1.3.2 Derivácia
vektorovej funkcie podľa času
Zavádza sa rovnako, ako derivácia funkcie jednej premennej, t.j. ako limita podielu. Napríklad derivácia polohového vektora r (t) sa definuje vzťahom:

(1.3.2.1)
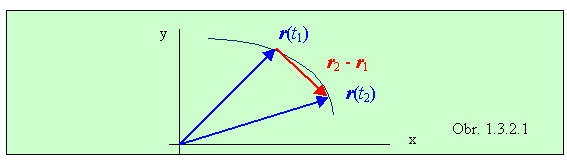
kde r1 a r2 sú polohové vektory (napr. pohybujúcej sa častice) v okamihoch t1 a t2 . Takto je definovaná okamžitá rýchlosť (častice), pomocou ktorej možno dobre pochopiť význam derivácie vektorovej funkcie. Na obrázku 1.3.2.1 sú nakreslené príslušné vektory, takže vidno smer i veľkosť vektora Dr . V limite pri t2 ® t1 sa vektor r2 približuje k vektoru r1 , takže vektor Dr sa skracuje a postupne sa svojim smerom približuje ku smeru dotyčnice krivky v bode s polohovým vektorom r1 . V definícii derivácie v menovateli zlomku vystupuje časový interval, teda skalárna veličina, takže podiel Dr/Dt je v podstate skalárnym násobkom vektora Dr , pričom násobiacim skalárom je zlomok 1/Dt . Preto výsledkom derivácie vektorovej funkcie podľa času je opäť vektorová funkcia, ktorej smer je určený čitateľom zlomku z definície derivácie. V tomto prípade smer vektora rýchlosti je totožný so smerom dotyčnice krivky v bode r1 . Veľkosť výsledku predstavuje veľkosť okamžitej rýchlosti (častice).
Pri konkrétnych výpočtoch derivácie vektorovej funkcie, keď chceme získať číselné hodnoty, treba vektorovú funkciu vyjadriť v zložkách, ako v (1.3.1.1). Napríklad polohový vektor pohybujúcej sa častice má potom tvar : r (t) = x(t) i + y (t) j + z(t) k . Takto zapísaná vektorová funkcia predstavuje súčet troch funkcií, preto deriváciu polohového vektora vyjadríme ako súčet derivácií jeho troch zložiek :
![]() (1.3.2.2)
(1.3.2.2)
V tomto výraze vystupujú zložky rýchlosti : vx i = (dx/dt) i atď. resp. súradnice vektora rýchlosti vx = (dx/dt) . Súradnica vektora rýchlosti predstavuje zmenu príslušnej súradnice polohového vektora pripadajúcej na jednotkový časový interval. Podľa definície derivácie platí
|
|
(1.3.2.3)
Táto derivácia môže byť kladná, i záporná (pravdaže i nulová). Kladná je vtedy, keď s pribúdajúcim časom rastie hodnota súradnice, záporná v opačnom prípade.
Význam "zlomku" dx/dt pochopíme na základe nasledujúcej úvahy. Ak častica za 1 s prejde napríklad 5 m, tak číselnú hodnotu rýchlosti častice vyjadríme ako podiel 5/1 = 5 . Táto častica za časový interval 0,1 s prejde 0,5 m , za 0,01 s 0,05 m atď. , ale podiel hodnôt 0,5/0,1 = 0,05/0,01 … atď. je stále rovnaký a zachová sa aj v limitnom prípade, keď hodnota menovateľa t2 - t1 sa blíži k nule. Preto výraz dx/dt vyjadruje zmenu súradnice pripadajúcu na jednotkový časový interval (sekundu). Takto treba chápať význam derivácie aj v iných prípadoch, keď v čitateli i v menovateli limity (1.3.2.3) sú iné premenné ako v tomto uvedenom príklade.
![]()
Príklad
1.3.2.1 Vypočítajte súradnice, zložky a veľkosť
rýchlosti častice, keď súradnice jej polohového vektora sú vyjadrené takto
: x
= p t , y = q + st
+ 0,5 ut 2 , z = 0,
pričom konštanty vo vzorcoch majú hodnoty p = -3 m/s ,
q = 4 m , s
= 2 m/s , u = - 9,81 m×s-2 .
Riešenie : Ak orientujeme os x vodorovne a os y zvislo, tak pozornejší čitateľ zistí, že ide
o šikmý vrh, zo začiatočnej výšky q = 4
m , začiatočnou rýchlosťou s = 2 m/s
nahor a rýchlosťou p = 3 m/s vodorovne v zápornom smere osi x
. Vyjadríme polohový vektor v zložkovom tvare : r(t) = pt i
+ (q + st + 0,5 ut2 ) j + 0 k
. Vektor rýchlosti získame
deriváciou polohového vektora, pričom použijeme vzorec (1.3.2.2) :
v = p i + (s
+ ut
) j ,
kde
vidno dve zložky vektora v
- zložku v smere vektora i a zložku v smere vektora j .
Pre súradnice vektora v pritom platí : vx = p =
-3 m/s , vy = s + ut =
(2 - 9,81 t ) m/s . To znamená, že súradnica vy sa mení s časom. Jej konkrétna číselná
hodnota závisí od časového údaja, ktorý do vzťahu pre súradnicu dosadíme.
Veľkosť vektora v získame, ak použijeme vzorec (1.1.4.3) : v = [p2 +
(s + ut )2]1/2
![]()
Kontrolné otázky
1.
Vyjadrite,
čo rozumieme pod deriváciou vektorovej funkcie podľa času !
2.
Výsledkom derivácie vektorovej funkcie podľa času je
funkcia vektorová, alebo skalárna ?
3.
Slovne vyjadrite, čo predstavuje veľkosť derivácie vektorovej
funkcie podľa času ?
4.
Vyjadruje derivácia vektorovej funkcie podľa času aj
smer výslednej vektorovej funkcie ?