1.2.4 Dvojnásobný vektorový súčin

Dvojnásobný vektorový súčin medzi tromi vektormi a, b, c môže mať dva tvary , pokiaľ dodržíme určené poradie vektorov :

a ´ (b ´ c) a (a ´ b) ´ c (1.2.4.1)

Zo zápisu je zrejmé, že výsledkom dvojnásobného vektorového súčinu je vektorová veličina. Uvedené dva tvary neposkytujú rovnaký výsledok. Výsledkom súčinu vektorov nachádzajúcich sa v zátvorke je v oboch prípadoch vektor , ktorý je na ich rovinu kolmý (označme si ho ako w , obr. 1.2.4.1). Súčinom vektora w s ďalším vektorom je vektor u, ktorý je kolmý aj na vektor w, takže u musí ležať v rovine vektorov, ktoré sú uvedené v zátvorke. To znamená, že výsledok dvojnásobného vektorového súčinu u možno vyjadriť ako lineárnu kombináciu vektorov, nachádzajúcich sa v zátvorke. V prvom prípade výsledný vektor u₁ leží v rovine vektorov b, c a v druhom prípade výsledný vektor u₂ leží v rovine vektorov a, b . Druhý prípad je nakreslený na obrázku.

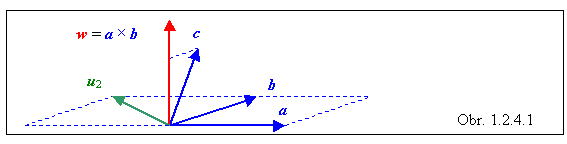
Pre výsledné vektory platia nasledujúce vzorce :

u₁ = a ´ (b ´ c) = b (a × c) - c (a × b ) (1.2.4.2)

u₂ = (a ´ b) ´ c = b (a × c) - a (b × c ) (1.2.4.3)

Správnosť týchto vzorcov možno dokázať celkom všeobecným postupom, ktorý je však náročný a pomerne rozsiahly. Preto si jeden zo vzorcov, a to (1.2.4.3) , odvodíme zjednodušeným postupom na príklade troch ľubovoľných nekomplanárnych vektorov a, b, c, v špeciálne zvolenej karteziánskej súradnicovej sústave. Súradnicovú os x zvolíme tak, aby bola rovnobežná s vektorom a , takže a bude mať len jednu zložku, a to rovnobežnú s jednotkovým vektorom i : a = a_x i . Os y zvolíme tak, aby rovina (xy) bola rovnobežná s rovinou určenou vektormi a, b . Vtedy vektor b , pokiaľ nie je kolmý na a , bude mať dve zložky : b = b_x i + b_y j . Os z karteziánskej sústavy je tým už jednoznačne určená, a tak vektor c , ak chceme uvažovať čo najvšeobecnejšie, musí mať tri zložky : c = c_x i + c_y j + c_z k

Súhrnne :

a = a_x i

b = b_x i + b_y j ,

c = c_x i + c_y j + c_z k (1.2.4.5)

Potom dvojnásobný vektorový súčin (a ´ b) ´ c vypočítame :

= [ a_x i ´ (b_x i + b_y j )] ´ (c_x i + c_y j + c_z k ) = [ a_x b_y k] ´ (c_x i + c_y j + c_z k ) =

= a_x b_y c_x j - a_x b_y c_y i + ( a_x b_x c_x i - a_x b_x c_x i )

Výraz v zátvorke v poslednom riadku nie je výsledkom priameho výpočtu, rovná sa nule, a to, že sme ho pridali do výpočtu, je len súčasťou nášho zjednodušeného postupu. Vhodným pospájaním členov posledného riadku dostaneme :

(a ´ b) ´ c = (a_x c_x) (b_x i + b_y j ) - (b_x c_x + b_y c_y) (a_x i) .

Keď si uvedomíme, že platí

a_x c_x = a × c a b_x c_x + b_y c_y = b × c ,

čo si ľahko overíme vypočítaním týchto skalárnych súčinov vychádzajúc zo zadania vektorov (1.2.4.5), dostaneme konečný výsledok

(a ´ b) ´ c = b (a × c) - a (b × c )

Podobne možno odvodiť aj vzorec (1.2.4.2), pričom opäť sa overí zásada, že výsledný vektor, výsledok dvojnásobného vektorového súčinu, možno vyjadriť ako lineárnu kombináciu vektorov ležiacich v rovine vektorov uvedených v zátvorke.

Dvojnásobný vektorový súčin sa často využíva pri vyjadrovaní vzťahov v mechanike, ale aj elektromagnetizme.

Príklad 1.2.4.1 Vypočítajte dvojnásobný vektorový súčin ( a ´ b) ´ c vektorov : a = 5 i , b = 4 i + 3 j , c = 2 i - j + k a overte si, že výsledný vektor leží v rovine vektorov a, b . Vektory a, b ležia v rovine xy , takže výsledný vektor by mal mať len zložky rovnobežné s jednotkovými vektormi i, j . Nakreslite si obrázok.

Riešenie : ( a ´ b) ´ c = [5 i ´ ( 4 i + 3 j )] ´ (2 i - j + k ) = [15 k] ´ (2 i - j + k ) =

= 30 j + 15 i

Kontrolné otázky

1. Napíšte dva možné varianty dvojnásobného vektorového súčinu !

2. V ktorej rovine leží výsledný vektor dvojnásobného vektorového súčinu ? Zdôvodnite svoje tvrdenie !

3. Napíšte vzorce vyjadrujúce výsledný vektor získaný dvojnásobným vektorovým súčinom !

4. Čím sa navzájom odlišujú výsledky súčinov (a x b) x c , c x (a x b) ?

5. Čím sa navzájom odlišujú výsledky súčinov (a x b) x c , a x (b x c) ?