1.2.3 Zmiešaný súčin

Zmiešaný súčin troch vektorov je operácia, v ktorej sa uskutoční najprv vektorový a po ňom skalárny súčin. Medzi tromi vektormi a, b, c je možných viacero variantov zmiešaného súčinu, napríklad :

a × (b ´ c), (a ´ b) × c , (b ´ c) × a (1.2.3.1)

Výsledkom je vždy skalárna veličina, ktorá môže byť kladná, nulová i záporná.

Niektoré vlastnosti zmiešaného súčinu .

· Výraz (a × b) ´ c , nie je zmiešaný súčin, lebo výraz v zátvorke je skalárna veličina, ktorou nemožno vektor c násobiť vektorovo.

· Zmiešaný súčin má význam objemu rovnobežnostena skonštruovaného na základe vektorov zmiešaného súčinu. Na obrázku 1.2.3.1 je nakreslený rovnobežnosten zostrojený pomocou vektorov a, b, c , ako aj priamka z   kolmá na rovinu vektorov a, b .

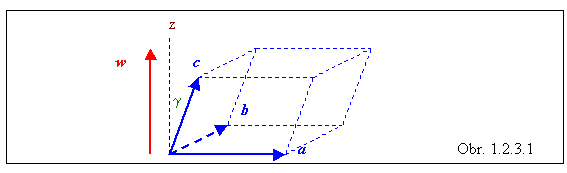
· Zmiešaný súčin

S = (a ´ b) × c vypočítame podľa pravidiel vektorového a skalárneho súčinu . Výsledkom vektorového súčinu a ´ b je vektor (označme ho w) kolmý na ich rovinu, teda vektor, ktorý má veľkosť ab sina a je rovnobežný s priamkou z . Vektor w zviera s vektorom c uhol g , ktorého kosínus vstupuje do výrazu pre skalárny súčin medzi vektormi w a c . Pre výsledok zmiešaného súčinu tak dostaneme S = (ab sina ) c cosg . Výraz c cosg súčasne predstavuje výšku rovnobežnostena, pričom veľkosť vektorového súčinu ab sina je plošný obsah jeho základne. Preto zmiešaný súčin má význam objemu rovnobežnostena.

· Rovnaký výsledok dostaneme aj pomocou zmiešaných súčinov (b ´ c) × a a (c ´ a) × b , teda súčinmi, v ktorých sme urobili cyklickú zámenu poradia vektorov, pri zachovaní polohy zátvoriek, ako aj značiek vektorového a skalárneho súčinu. Preto platia rovnosti

(a ´ b) × c = (b ´ c) × a = (c ´ a) × b (1.2.3.2)

· Ak si uvedomíme komutatívnosť skalárneho súčinu, môžeme napísať rovnosť

(a ´ b) × c = c × (a ´ b) (1.2.3.3)

Porovnaním posledných členov  rovností (1.2.3.2) a (1.2.3.3) dostaneme výsledok

(c ´ a) × b = c × (a ´ b) (1.2.3.4)

ktorý interpretujeme ako možnosť premiestnenia zátvoriek, pri súčasnej výmene značiek vektorového a skalárneho súčinu.

· Zmiešaný súčin je kladný, ak vektory v zmiešanom súčine, v takom poradí ako sú napísané, tvoria pravotočivú sústavu. Zámenou poradia ľubovoľných dvoch vektorov v zmiešanom súčine, zmení sa jeho znamienko. Ak je zmiešaný súčin záporný, objemu rovnobežnostena sa vtedy rovná jeho absolútna hodnota.

· Nulová hodnota zmiešaného súčinu znamená, že príslušné vektory sú komplanárne.

· Zmiešaný súčin možno vyjadriť pomocou determinantu, pričom v jednom riadku sú súradnice jedného vektora. K tomuto tvrdeniu môžeme dospieť, keď si všimneme zápis vektorového súčinu pomocou vzťahov (1.2.2.6) a (1.2.2.7) . Ak výraz (1.2.2.6) skalárne vynásobíme vektorom c = c_x i + c_y j + c_z k , dostaneme

(c_x i + c_y j + c_z k ) × [i ( a_yb_z - a_zb_y ) + j ( a_zb_x - a_xb_z ) + k ( a_xb_y - a_yb_x )] =

= c_x ( a_yb_z - a_zb_y ) + c_y ( a_zb_x - a_xb_z ) + c_z ( a_xb_y - a_yb_x ),

takže je zrejmé, že tento zmiešaný súčin možno vyjadriť ako determinant

(1.2.3.5)

Zápisom zmiešaného súčinu v tvare determinantu možno overiť pravidlo o cyklickej zmene poradia vektorov, ako aj o zmene znamienka pri zámene poradia dvoch vektorov. Zámena poradia dvoch vektorov sa v determinante prejaví ako zámena dvoch riadkov, ktorej dôsledkom je zmena znamienka determinantu.

Príklad 1.2.3.1 Vypočítajte zmiešaný súčin c × (a ´ b) pričom vektory sú zadané v zložkovom tvare : a = 5 i , b = 4 i + 3 j , c = 2 i - j + k . Overte si, že rovnaký výsledok dostanete, ak v zmiešanom súčine urobíte cyklickú zámenu poradia vektorov.

Riešenie : Výpočtom vektorového súčinu sa presvedčíme, že (a ´ b) = 15 k . Výsledok vynásobíme skalárne vektorom c : (15 k ) × (2 i - j + k ) = 15 .

Pre zmiešaný súčin (c ´ a) × b dostaneme rovnaký výsledok : (2 i - j + k ) ´ (5i ) = 5k + 5 j a ďalej (5k + 5 j ) × (4 i + 3 j ) = 15 .

Kontrolné otázky

1. Uveďte možné varianty zmiešaného súčinu troch vektorov !

2. Aký je geometrický význam zmiešaného súčinu ? Zdôvodnite svoje tvrdenie !

3. Viete zdôvodniť pravidlo o posune zátvoriek a súčasnej zámene "bodky a krížika" v zmiešanom súčine ?

4. Kedy je zmiešaný súčin kladný, záporný, nulový ?

5. Vyjadrite zmiešaný súčin troch vektorov v tvare determinantu !

6. Čo sa zmení na zmiešanom súčine, ak v ňom zmením poradie dvoch vektorov ?