1.1.4
Zložky a súradnice vektora
Rozklad vektora na zložky je opačná operácia ako súčet vektorov. V rovine možno vektor rozložiť na dve zložky, t.j. na dva vektory do vopred určených smerov. Sčítaním zložiek vznikne pôvodný vektor. Na obr. 1.1.4.1 je znázornený rozklad vektora a do smerov naznačených dvomi priamkami. Uskutočňuje sa tak, že priamky, do smerov ktorých treba vektor rozložiť, vedieme koncovým aj začiatočným bodom vektora. Tak vznikne rovnobežník, na ktorom už jednoducho vyznačíme zložky p a q .
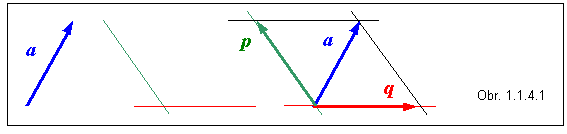
V priamkach, do ktorých rozkladáme vektor a , môžeme zvoliť jednotkové vektory, ktoré označíme e1 a e2 . Jednotkovými vektormi sú potom určené príslušné smery. Zložky p a q vyjadríme ako skalárne násobky vektorov e1 a e2 : p = ape1 , q = aqe2 . Vektor e1 však môže mať opačný smer ako zložka p , a vtedy skalár ap pred vektorom e1 musí byť záporný. Preto skalár ap nepredstavuje veľkosť vektora p, ale je jednou zo súradníc rozloženého vektora a vo vzťažnej sústave určenej vektormi e1 a e2 . Vektor a možno po takomto rozklade na zložky vyjadriť v tvare
a = p + q = ape1 + aqe2 . (1.1.4.1)
O takomto vyjadrení hovoríme, že vektor a je lineárnou kombináciou vektorov e1 a e2 .
V trojrozmernom priestore musí byť vzťažná sústava určená tromi
vektormi e1 , e2 a e3 o ktorých hovoríme, že tvoria jej bázu . Vo všeobecnosti to ani nemusia byť
jednotkové vektory. Najčastejšie sa
však používa rozklad do troch navzájom kolmých smerov, určených jednotkovými
vektormi so zaužívaným označením i, j, k
. Stotožňujú sa s osami x, y, z karteziánskej súradnicovej sústavy.
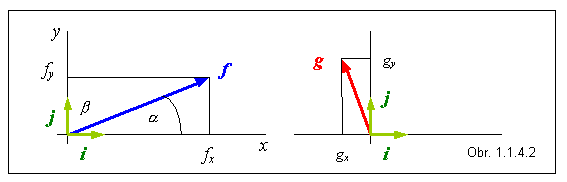
Ľubovoľný vektor f možno
pomocou takejto trojice jednotkových vektorov vyjadriť ako ich lineárnu
kombináciu
f = fx i + fy j + fz k . (1.1.4.2)
V tomto vyjadrení vektora f sú fx , fy a fz jeho súradnice, ktoré môžu byť kladné, i záporné podľa toho, aký je jeho smer vzhľadom na jednotkové vektory. Na obr. 1.1.4.2 je znázornený dvojrozmerný prípad, pričom vektor g má zápornú súradnicu gx , ostatné súradnice vektorov f a g sú kladné.
|
|
Veľkosť vektora f možno v karteziánskej súradnicovej sústave vyjadriť pomocou jeho súradníc, použitím Pythagorovej vety
![]() . (1.1.4.3)
. (1.1.4.3)
Vektor f zviera s vektormi i , j , k smerové uhly a , b , g , pre ktoré platia vzťahy
![]() ,
,
(1.1.4.4)
ktoré si možno overiť na dvojrozmernom obrázku 1.1.4.2 .
Zo vzťahov (1.1.4.4) pre kosínusy smerových uhlov (smerové kosínusy) bezprostredne vyplýva rovnosť
cos2a + cos2b + cos2g = 1 (1.1.4.5)
Súčet vektorov a skalárny násobok vektora možno výhodne počítať, keď vektory vyjadríme v zložkovom tvare. Napríklad ak a = ax i + ay j + az k , b = bx i + by j + bz k potom môžeme ich súčet uskutočniť po zložkách, na základe platnosti komutatívnosti a asociatívnosti sčítania vektorov :
a + b = ( ax+ bx) i + (ay + by) j + (az + bz ) k , (1.1.4.6)
takže pre súradnice výsledného vektora c platí
cx = ( ax+ bx) , cy = (ay + by) , cz = (az + bz ) . (1.1.4.7)
Pre skalárny násobok vektora vyjadreného v zložkách platí :
d = sa = s ( ax i + ay j + az k ) = sax i + say j + saz k ,
pričom pre jeho
súradnice platí dx = sax , dy
= say , dz = saz
. (1.1.4.8)
__________________________________
Príklad
1.1.4.1 Vypočítajte súčet
vektorov a = 3 i + 2 j - k
a b = -i + 2 j - 2 k
.
Riešenie
: c = a + b =
(3 - 1)i + (2 + 2)j
+ (-1 -2)k = 2 i + 4j - 3k
, takže súradnice vektora c sú :
cx = 2 , cy = 4 , cz = -3 .
Príklad 1.1.4.2 Vyjadrite vektor
d, ktorý má trojnásobnú
veľkosť a opačný smer ako
vektor a = 3 i + 2 j - k .
Riešenie
: d = (-3)a
= (-3)(3 i + 2 j - k ) = -9 i - 6 j
+ 3k . Presvedčite sa , že
veľkosť vektora d je naozaj trojnásobná v porovnaní s
veľkosťou vektora a .
__________________________________
Kontrolné otázky
1.
Ako rozkladáme vektor (v rovine) do dvoch vopred
zadaných smerov ?
2.
Možno vektor
rozložiť do dvoch smerov, ktoré zvierajú uhol väčší než 90 o ?
3.
Uveďte čo
rozumieme pod lineárnou kombináciou vektorov !
4.
Uveďte, čo je báza vektorov !
5.
Ako sa vypočíta veľkosť vektora, keď sú známe jeho
súradnice ?
6.
Ako sa zmenia zložky vektora, keď ho vynásobíme
skalárom ?
7.
Ako sa zmenia súradnice vektora, keď ho vynásobíme
skalárom ?
8.
Vyjadrite súčet dvoch vektorov pomocou ich súradníc
!
9.
Uveďte, ako vypočítate uhol ktorý vektor zviera s
osou y, keď poznáte jeho súradnice !