1.1.2 Súčet a rozdiel vektorov

Súčet dvoch vektorov a + b = c je operácia, ktorej výsledkom je opäť vektor. Graficky sa znázorňuje pomocou úsečiek zobrazujúcich vektory : ku koncu prvého vektora pripojíme druhý vektor, pričom výsledkom ich sčítania je tretí vektor, ktorého začiatok je zhodný so začiatkom prvého vektora a koniec s koncom druhého vektora . V grafickom znázornení :

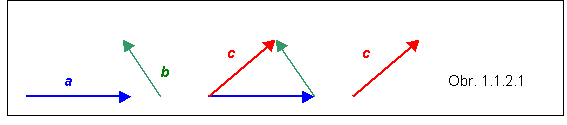
Analogicky sa pokračuje pri sčítaní viacerých vektorov.

Súčet vektorov je komutatívna operácia, čiže výsledok súčtu nezávisí od poradia skladania vektorov :

a + b = b + a . (1.1.2.1)

Pri sčítaní viacerých vektorov sa uplatňuje asociatívnosť, ktorú v prípade troch vektorov možno vyjadriť vzťahom

a + b + c = (a + b) + c = a + (b + c) (1.1.2.2)

Ak pred vektor napíšeme znamienko "mínus", napríklad - a , podľa zaužívanej dohody to predstavuje vektor, ktorý má rovnakú veľkosť ako vektor a , ale má opačný smer. Nový vektor možno označiť ako vektor b, a zapísať rovnosť b = - a . Vektory a , b sú teda kolineárne.

Takéto označenie umožňuje zaviesť odčítanie (rozdiel) vektorov. Rozdiel dvoch vektorov c - d = f chápeme ako súčet vektorov c a (- d), t.j. f = c + (- d) . Pritom rovnicu c - d = f možno upraviť rovnako, ako rovnicu s obyčajnými číslami, napríklad vektor d previesť na pravú stranu rovnice : c = d + f . Takto upravená rovnica môže poslúžiť na overenie správnosti vykonanej operácie.

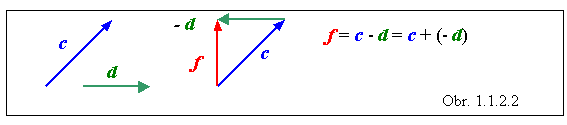
Na súčte vektorov si možno názorne ukázať význam používania vektorového označovania. Ak pri súčte dvoch vektorov platí rovnosť a + b = c , kde a , b nie sú kolineárne vektory, potom pre ich veľkosti platí trojuholníková nerovnosť a + b > c. Keby sme vynechali označenie vektorov, napísali by sme nesprávnu rovnicu a + b = c . Dôsledné používanie označovania vektorov je preto veľmi dôležité.

_________________________________

Príklad 1.1.2.1 Dva nekolineárne vektory, napr. a, b , môžeme chápať ako strany rovnobežníka. Graficky ukážte, že ich súčet a rozdiel predstavujú uhlopriečky tohto rovnobežníka.

Riešenie :

_________________________________

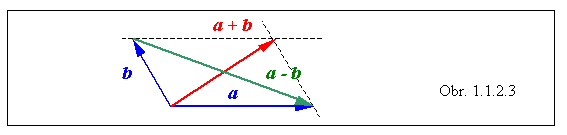
Súčet vektorov má časté uplatnenie v praxi. Napríklad sčítaním vektora rýchlosti lode vzhľadom na vodu s vektorom rýchlosti vody v rieke, dostaneme vektor rýchlosti lode vzhľadom na breh rieky.

_________________________________

Príklad 1.1.2.2 Nakreslite štvoruholník, ktorého strany nie sú rovnako dlhé. Dokážte, že ak by sa uhlopriečky štvoruholníka pretínali vo svojich stredoch, musel by to byť rovnobežník. (Obr. 1.1.2.4)

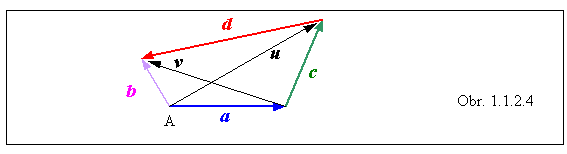
Riešenie : Najprv treba označiť všetky štyri strany štvoruholníka ako vektory. Podľa obrázku dokážeme určiť vektory smerujúce z vrcholu A do stredov uhlopriečok. Do stredu uhlopriečky u smeruje vektor p = (1/2) u = (1/2)(a + c) a do stredu uhlopriečky v vektor q = a + (1/2)(b - a) = (1/2)(a + b) . Ak majú byť stredy uhlopriečok totožné, musia byť vektory p a q rovnaké : (1/2)(a + c) = (1/2)(a + b) , z čoho bezprostredne vyplýva rovnosť vektorov b a c . Majú teda rovnakú veľkosť aj smer, preto sú rovnobežné, tvoria dve strany rovnobežníka. Výsledok pre ďalšie dve strany získame úvahou o vektore u. Platí u = c + a a súčasne u + d = b, čiže u = b - d a s využitím rovnosti b = c aj u = c - d . Porovnaním dvoch vyjadrení vektora u dospejeme k výsledku a = - d . Teda aj tieto vektory sú rovnobežné, majú rovnakú veľkosť, ale opačný smer.

_________________________________

Kontrolné otázky

1. Slovne vyjadrite postup pri grafickom sčítaní dvoch vektorov

2. Ovplyvní zámena poradia vektorov pri súčte výsledok ?

3. Je sčítanie dvoch vektorov komutatívna operácia ?

4. Je sčítanie viacerých vektorov asociatívna operácia ?

5. Na príklade názorne vysvetlite asociatívnosť súčtu vektorov !

6. Čo znamená znamienko mínus pred vektorom ?

7. Ako je definované odčítanie dvoch vektorov ?

8. K akým dôsledkom môže viesť nepoužívanie označenia vektorov ?

9. Uveďte príklad z praxe, kde sa uplatňuje sčítanie vektorov !