TEST č. 2

1.
Uveďte dva príklady
vektorových veličín z kinematiky
a napíšte vzťah pre ich veľkosť a smer.
2.
Napíšte príklad fyzikálnej veličiny určenej vektorovým
súčinom. Napíšte aj jej jednotku.
3.
Na obrázkoch č. 1 a 2 sú nakreslené časové závislosti
rýchlosti a dĺžky ubehnutej dráhy pri priamočiarom pohybe. Charakterizujte
pohyb telesa odpovedajúci týmto grafom v jednotlivých časových
intervaloch.
4.
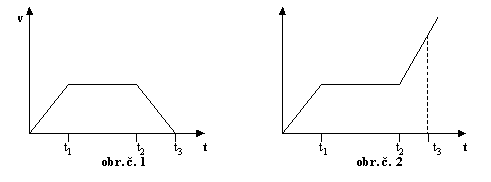
Napíšte
akými rýchlosťami sa pohybuje teleso, ktorého časová závislosť dĺžky ubehnutej
dráhy pozdĺž priamky je znázornená na obr. č. 2.
5.
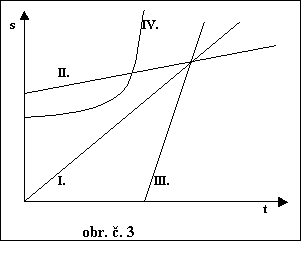
Rozhodnite aký typ pohybu, ktorého časová závislosť je
znázornená
grafmi na obr. č. 3
(s je dĺžka
ubehnutej dráhy, t je čas). Napíšte jeho matematické
vyjadrenie pre každý prípad.
6.
Z obr. č. 3. vysvetlite:
a) čo znamená priesečník grafu
s jednotlivými osami;
b) čo znamenajú priesečníky
grafov;
c) ktoré z telies I., II.
III. má najväčšiu rýchlosť.
Svoju voľbu zdôvodnite!
7.
Čo možno povedať o dvoch vektoroch, ktorých skalárny
súčin je rovný nule? Uveďte príklad.
8.
Určite veľkosť a smer vektora rýchlosti pri krivočiarom
pohybe.
9.
Pri krivočiarom pohybe rozkladáme vektor zrýchlenia do dvoch
význačných smerov. Napíšte a aké dva smery sa jedná a matematicky
formulujte vzťahy pre zrýchlenie v týchto smeroch.
10.Ak hmotný
bod koná rovnomerný pohyb po kružnici, aké má celkové zrýchlenie?
11.Ktoré
z uvedených závislostí popisujú pohyb s nenulovým konštantným
zrýchlením? ( Veličiny: t – čas, v – veľkosť rýchlosti, s –
dĺžka dráhy.)
a)
v = 3 + 2t
b)
v = 10
c)
s = 3 + 2t
d)
s = 3t –t2
e)
s = 1-2t
12.Na aké
zložky zvyčajne rozkladáme zrýchlenie? Napíšte ich matematické vyjadrenie.
13.Aké je celkové
zrýchlenie pri rovnomernom pohybe po kružnici?
14.Čo je
veľkosť a aký je smer vektora uhlovej rýchlosti stáčania polohového
vektora?
15.Napíšte
vzťah medzi obvodovou a uhlovou rýchlosťou. Nakreslite ich vo zvolenej
súradnicovej sústave.
Dodržali ste 30 min časový limit? Dosiahli ste
minimálne 50 % úspešnosť? V tejto
časti si ozrejmíme, či
získané vedomosti : ·
ste schopný/á/ aplikovať na riešenie fyzikálnych problémov; ·
viete
matematicky formulovať a zhodnotiť ich na konkrétnom prípade; ·
uplatníte len pri jednoduchších príkladoch; ·
uplatníte
aj pri náročnejších príkladoch.
