8.2 Vodič v elektrostatickom poli

Potrebné vedomosti

Pochopenie tejto kapitoly, vyžaduje poznať pojmy z elektrostatiky, ako je Coulombova sila, intenzita elektrického poľa, potenciál, ale predovšetkým chápať obsah a vedieť aplikovať Gaussov zákon elektrostatiky.

Učebné ciele

Študent by mal vedieť popísať vlastnosti vodiča, vysvetliť jav elektrostatickej indukcie. Po preštudovaní látky by mal vedieť kvalitatívne a kvantitatívne popísať elektrické pole v okolí vodivého telesa ktoré je vložené do elektrického poľa a pole v okolí nabitého vodiča. Na príkladoch by mal vedieť vysvetliť princíp elektrostatického tienenia.

Kľúčové slová

vodič, elektrostatická indukcia, povrchový náboj, Coulombova veta, elektrostatické tienenie, sršanie elektriny

V hrubých rysoch možno telesá rozdeliť podľa pohyblivosti nabitých častíc, z ktorých sa teleso skladá (elektrónov, iónov) na vodiče, izolanty a polovodiče. Vodiče sú látky s veľkou hustotou voľne sa pohybujúcich sa nábojov. Príkladom sú kovy, v ktorých je rádovo 10²⁹ elektrónov / m³, čo predstavuje pohybujúci sa náboj 10¹⁰ C v jednom kubickom metri vodiča. Izolanty, sú dielektrické látky u ktorých je hustota voľných nábojov zanedbateľne malá a voľný pohyb naboja nie je možný. Polovodiče sú látky s relatívne malou hustotou voľného náboja, ktorá výrazne závisí od štruktúry polovodiča a rádovo sa mení zmenou teploty polovodiča.

8.2.1 Pohyblivosť nábojov vo vodičoch

Voľne sa pohybujúce elektróny v mriežke iónov kovu predstavujú plyn, pre ktorý stredná kvadratická rýchlosť tepelného pohybu elektrónu je rádovo 10⁶ m s^-1. Elektrón sa pohybuje chaotickým tepelným pohybom, vymieňa svoju energiu s časticami elektronového plynu a iónovou mriežkou látky.

Vložením vodiča do elektrického poľa pôsobí na elektrón elektrická sila, ktorá mení jeho hybnosť. Prírastok rýchlosti elektrónu k jeho tepelnej rýchlosti je pomerne malý, pretože po krátkej strednej vzdialenosti dochádza k zrážke s prekážkou v mriežke, elektrón odovzdáva svoju energiu a pohybuje sa v novom smere tepelným pohybom. Aj keď model častice klasickej mechaniky nie celkom vystihuje podstatu pohybu elektrónov, v hrubých rysoch môžeme určiť strednú rýchlosť unášania elektrónov v, z pohybovej rovnice:

, (8.2.1.1)

silu F pôsobiacu na elektrón určuje intenzita elektrického poľa E, hybnosť elektrónu p určuje súčin jeho efektívnej hmotnosti m_ef a okamžitej rýchlosti v, v_o je počiatočná rýchlosť elektrónu po predchádzajúcej zrážke, v_max je rýchlosť v okamihu nasledujúcej zrážky. Rýchlosť unášania elektrónov má opačný smer vzhľadom na intenzitu elektrického poľa (náboj elektrónu je záporný) a z rovníc vyplýva:

, (8.2.1.2)

kde t je stredná doba medzi dvomi zrážkami.

Pohyblivosť voľného náboja vo vodiči zavádzame ako koeficient úmernosti medzi strednou rýchlosťou unášania a intenzitou elektrického poľa:

. (8.2.1.3)

Pretože so zvyšujúcou teplotou sa zväčšuje chaotický pohyb elektrónového plynu i kmitanie mriežky, doba t sa skracuje a pohyblivosť klesá.

Obr. 8.2.2.1

Zmena elektrického poľa po vložení vodivého telesa do homogénneho poľa.

8.2.2 Rozloženie nábojov v ustálenom stave

Vložme vodivé teleso, ktoré je elektricky neutrálne, t.j. je v ňom rovnováha medzi kladnými a zápornými nábojmi, do elektrického poľa intenzity E. Vplyvom síl, pôsobiacich na voľné náboje sa tieto začnú premiestňovať v telese tak až vytvoria vo vnútri vodiča indukované elektrické pole E_i, ktoré v každom bode vo vnútri vodiča kompenzuje vonkajšie elektrické pole E (8.2.2.1). Uvedomme si, že napr. v kove je v 1 cm³ asi 10²³ voľných elektrónov, čo predstavuje náboj 10⁴ C. Takýto náboj sústredený do bodu by vytvoril vo vzdialenosti 1 cm pole nepredstaviteľne veľkej intenzity 10¹⁶ V m^-1 (blesk v atmosfére Zeme vzniká už pri intenzitách menších o desať rádov). Preto len nepatrná časť náboja sa premiestni, ako uvidíme ďalej, na povrch vodiča tak, že výsledné pole vo vodiči je nulové a náboje sa ďalej usporiadaným pohybom nepremiestňujú. Ak by sme teraz, pôvodne nenabité teleso vhodne rozdelili na dve časti, dostali by sme dve nabité telesá s nenulovým nábojom i po vybraní z vonkajšieho poľa. V jednej časti bude prevaha záporného náboja elektrónov na kladnými iónmi, v druhej ich nedostatok a táto časť bude nabitá kladne. Tento jav nabíjania telesa vonkajším elektrickým poľom nazývame elektrostatická indukcia.

Obr. 8.2.2.2

Rozloženie náboja na plochách povrchu vodivého telesa

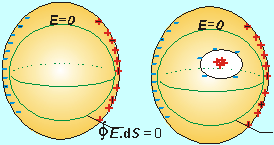
Elektrické pole vo vodiči, vytvorené vonkajším a indukovaným poľom má nulovú intenzitu. Ak by nebola nulová, spôsobovala by ďalšie premiestňovanie náboja až do stavu nastolenia rovnováhy. Tento stav rovnováhy nastáva veľmi rýchle. Elektrostatika neskúma priamo tieto zmeny, ale sleduje až konečné rovnovážne stavy.

Z Gaussovej vety jednoducho dokážeme, že nenulový náboj je len v povrchu telesa, vytvorí sa tzv. povrchový elektrický náboj. Ak by sme si volili ľubovoľnú uzatvorenú plochu, ktorá cela leží vo vnútri telesa (Obr.8.2.2.2), potom tok intenzity touto plochou je nulový:

,

pretože intenzita vo vnútri telesa je nulová. Preto aj náboj v časti telesa, uzatvoreného touto plochou je nulový (je nastolený stav rovnováhy kladných a záporných nábojov). To platí pre každú ľubovoľnú malú časť (samozrejme makroskopicky malú) vnútrajška telesa. Rozloženie náboja na povrchu charakterizuje plošná hustota náboja

Rozoberme ešte prípad, že v telese je dutina, v ktorej môže byť viazaný náboj. V tomto prípade by viazaný naboj v dutine bol kompenzovaný rovnako veľkým nábojom rozloženým na vnútornej stene telesa.(Obr.8.2.2.2). Pole viazaného náboja v dutine sa neprejaví na vonkajšej strane telesa. Naopak vonkajšie pole je tienené v dutine nábojom rozloženým z vonkajšej strany vodivého telesa. Pretože kompenzácia prerozdelením voľného náboja prebieha rýchle, rádovo v časových intervaloch 10^-14 s až 10^-12 s týmto spôsobom možno odtieniť aj vysokofrekvenčné elektrické pole. To sa uplatňuje napríklad v konštrukcii koaxiálneho kábla. Vnútorný vodič je obkolesený vonkajším valcovým vodičom (sieťkou) ktorý plní úlohu tienenia rušivých elektrických polí.

8.2.3 Elektrické pole vo vnútri a na povrchu vodičov

Obr. 8.2..3.1

Ekvipotenciálne plochy elektrického poľa

Elektrické pole, ktoré vzniklo okolo vodivého telesa vo vonkajšom elektrickom poli z predchádzajúceho príkladu, možno vyjadriť aj potenciálom. Predovšetkým si musíme uvedomiť, že každý bod vodivého telesa má rovnaký potenciál. Keďže intenzita elektrického poľa vo vodiči je nulová, aj rozdiel potenciálov ľubovoľných bodov vodivého telesa je nulový:

.

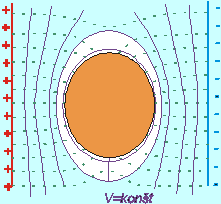
Celé teleso predstavuje jednu ekvipotenciálnu hladinu. Siločiary elektrického poľa sú kolmé na ekvipotenciálne plochy, preto intenzita elektrického poľa je na povrch vodivého telesa kolmá. Tvar ekvipotenciálnych hladín je na Obr.8.2.3.1.

Pre elektrické pole tesne nad povrchom vodiča platí Coulombova veta: Elektrická intenzita nad povrchom vodiča je kolmá na povrch vodiča a úmerná plošnej hustote náboja. Konštanta úmernosti je prevrátená hodnota elektrickej konštanty (permitivity vákua).

(8.2.3.1)

Pritom na zakrivených plochách je hustota náboja s nepriamoúmerná polomeru krivosti plochy R (Plošná hustota náboja na zakrivených plochách )

s R = konst (8.2.3.2)

Coulombova veta - odvodenie

Príklad 8.2.1 Do elektrického poľa bodového náboja Q je vložená vodivá rovinná doska veľmi veľkých rozmerov. Nakreslite tvar siločiar na oboch stranách dosky, ak doska a) nie je uzemnená, b) je uzemnená. Aké bude v týchto prípadoch rozloženie elektrického náboja na oboch povrchoch tejto dosky (kvalitatívne)?

Riešenie

Príklad 8.2.2 Aký maximálny celkový náboj možno umiestniť na osamelej vodivej guli s polomerom R = 2 m, ak nemá dôjsť k sršaniu elektriny z hrotu umiestnenom na povrchu gule. Polomer zakrivenia hrotu je 1 cm (sršanie nastáva v mieste gule, kde intenzita poľa nad povrchom je 3.10⁶ V m^-1)

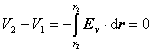Riešenie

Kontrolné otázky