13.1.2.2 Zákon vyžarovania pre absolútne čierne teleso

Rayleigh a Jeans skúmali žiarenie absolútne čiernych telies a zistili, že v stacionárnom stave spektrálna hustota intenzity tepelného vyžarovania M_l vystupujúceho kolmo z jednotkového objemu dutiny absolútne čierneho telesa, šíriaca sa v jednotkovom priestorovom uhle a pripadajúcu na interval vlnových dĺžok < l , l + dl > je určená vzťahom

(13.1.2.5)

kde k je Boltzmannova konštanta, T je teplota absolútne čierneho telesa. Vzťah (13.1.2.5) sa nazýva Rayleighov a Jeansov zákon vyžarovania pre absolútne čierne teleso, ktorého odvodenie čitateľ nájde v odkaze. Tento zákon možno vyjadriť i v závislosti od frekvencie vlnenia f.

_________________________________________

Príklad.13.1.2.5 Odvoďte z Rayleighovho a Jeansovho zákona, určeného vzťahom (13.1.2.5), Rayleighov a Jeansov zákon ako funkciu frekvencie a absolútnej teploty.

Riešenie: Na základe odvodenia Rayleighovho a Jeansovho zákona vieme, že energia vyžiarená jednotkovým objemom dutiny absolútne čierneho telesa je funkciou vlnovej dĺžky l a teploty T v tvare

. ( 1 )

Zo vzťahu l = c / f , kde c je rýchlosť svetla a f frekvencia vlnenia dostaneme :

. ( 2 )

Pretože zväčšeniu frekvencie zodpovedá zmenšenie vlnovej dĺžky je

M_l (l,T) dl = - M _f ( f ,T) df . ( 3 )

Po dosadení predchádzajúcich vzťahov do rovnice ( 1 ) dostaneme

,

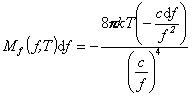a jej úpravou dostávame vzťah

, (13.1.2.6)

ktorý vyjadruje Rayleighov a Jeansov zákon ako funkciu frekvencie a absolútnej teploty.

_____________________________________

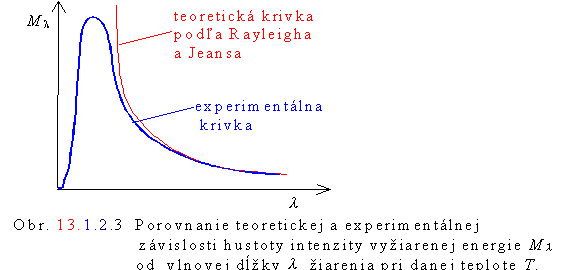
Rayleighov a Jeansov zákon žiarenia pomerne dobre vystihoval experimentálne údaje pre veľké vlnové dĺžky ( infračervenú oblasť). Nameraná závislosť spektrálnej hustoty intenzity vyžarovania M_l odhalila rozdiel pre krátkovlnnú oblasť (obr. 13.1.2.3), kde sa pozoroval pokles M (l) d l ® 0 pri prechode do ultrafialovej oblasti spektra (lim l® 0 ). Rayleighov a Jeansov zákon predpovedá narastanie intenzity do nekonečna. Nárastu intenzity v oblasti krátkych vlnových dĺžok bol priradený názov „ultrafialová katastrofa“. Nesúlad teórie s experimentov znamená, že niektorý z použitých predpokladov pri výpočtoch Rayleigha a Jeansa nebol správny.

Odpovedať na túto otázku, ktorý z predpokladov nebol správny, sa podarilo Maxovi Planckovi v roku 1900. Tento nesúlad teórie a experimentu nebolo možné vysvetliť na základe klasickej elektrodynamiky a viedol Maxa Plancka k hľadaniu matematickej formulácie pre žiarenie absolútne čierneho telesa. Ním odvodená zákonitosť, spolu s fyzikálnym vysvetlením, sa stala základným kameňom pre vybudovanie kvantovej fyziky.

Pri odstraňovaní rozporu teoreticky odvodenej krivky, určenej Rayleighovým a Jeansovým zákonom, Max Planck vychádzal z predpokladov:

· ekvipartičná teoréma platí len pre spojité rozdelenie možných energií;

· pripustil hypotézu, že energia elektromagnetickej vlny s frekvenciou f sa nevyžaruje

z atómov spojito, ale je v skutočnosti kvantovaná, t.j. emitovaná po malých množstvách,

ktoré nazval kvantá;

· molekuly emitujú energiu v diskrétnych jednotkách svetelnej energie preskokom

z jedného stavu do druhého;

· molekuly budú žiariť alebo absorbovať energiu len keď zmenia kvantový stav;

· zaviedol jednotku kvanta energie E = hf, , kde h = 6,624 . 10^-34 J.s je Planckova

konštanta; ktorá znamená, že ak sa kvantové číslo zmení o 1, množstvo vyžiarenej energie

molekulou bude hf;

· predpokladal, že kmitajúce molekuly (oscilátory), ktoré emitujú žiarenie, môžu nadobúdať

len isté diskrétne hodnoty energie E_n = nhf, kde kvantové číslo n = 1, 2, .... ;

· ak molekuly ostávajú v danom stave, žiadna energia sa neabsorbuje ani nevyžaruje.

Planckova konštanta h, resp. redukovaná Planckova konštanta (čítaj há-trans), definovaná vzťahom

je základná konštanta mikrosveta a teda kvantovej fyziky. Hrá obdobnú úlohu ako konečná hodnota rýchlosti svetla c v relativistickej fyzike. Keby c nebola konečná hodnota, nevznikla by teória relativity. Rovnako je tomu aj v prípade Planckovej konštanty. Keďže je síce malá, ale rôzna od nuly, má za následok kvantovanie hodnôt viacerých fyzikálnych veličín v mikrosvete.

Myšlienka kvantovania energie, t.j. existencia diskrétnych energetických stavov, sa stala základom pre vznik kvantovej mechaniky.

V roku 1905 túto myšlienku rozšíril Albert Einstein o hypotézu, že pri emisii alebo absorpcii svetla atómov sa energia nielen vyžaruje, ale aj šíri prostredím po kvantách hf. Kvantum energie E = hf sa od roku 1926 nazýva fotón. (Zavedenie tohto pojmu prináleží A. Comptonovi .)

Z predpokladu, že atómy emitujú a absorbujú žiarenie v energetických kvantách o veľkosti hf, pričom preskakujú z jedného energetického stavu do druhého a menia svoju energiu o hodnotu hf , vyjadril M. Planck spektrálnu hustotu intenzity vyžarovania M (f) df vzťahom, ktorý nazývame Planckov zákon žiarenia:

kde c je rýchlosť svetla, k Boltzmannova konštanta, T teplota čierneho telesa a f frekvencia žiarenia. Odvodenie Planckovho zákona pre energiu vyžiarenú jednotkovým objemom absolútne čierneho telesa pri teplote T do jednotkového priestorového uhla a pripadajúcu na žiarenie s frekvenciou z intervalu (f, f + df), čitateľ nájde v hypertexe. Ak dosadíme Planckov získaný výsledok (13.1.2.8) do rovnice (13.1.2.1), dostaneme celkovú intenzitu vyžarovania (excitanciu) vo vnútri dutiny

kde a je univerzálna konštanta. Posledná rovnica výpočtom potvrdzuje experimentálny poznatok, formulovaný Stefanovým a Boltzmannovým zákonom, určeným rovnicou (13.1.2.4).

Poznámka: Na základe klasickej fyziky nebolo možné vysvetliť Wienov posuvný zákon, t.j. prečo sa maximum spektrálnej hustoty so zvyšujúcou sa teplotou posúva ku kratším vlnovým dĺžkam. Táto skutočnosť vyplýva z Planckovho zákona, ak hľadáme extrém funkcie (13.1.2.8). Riešením rovnice dM_l (l)/dl = 0 možno získať Wienov posuvný zákon určený rovnicou (13.1.2.2).

_____________________________________________________

Príklad 13.1.2.5 Vypočítajte koľkokrát viac energie vyžiari absolútne čierne teleso zahriate na teplotu T = 3 000 K v infračervenej oblasti s vlnovou dĺžkou l₁ = 9,6.10^-7 m, než vo viditeľnej oblasti pre l₂ = 6.10^-7 m.

Riešenie: Spektrálna hustota intenzity žiarenia absolútne čierneho telesa je určená Planckovým zákonom (13.1.2.6)

.

Pre vyžarovanie s vlnovou dĺžkou l₁ , resp. l₂ pri danej teplote T platí

.

.

Pre pomer spektrálnych hustôt intenzity pri danej teplote T dostávame

.

–––––––––––––––––––––––––––––––––––

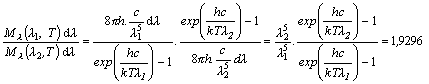Kontrolné otázky

1. Ktorý z predpokladov použitých pri odvodzovaní Rayleighovho a Jeansovho zákona bol správny?

2. Ktorý z predpokladov použitých pri odvodzovaní Rayleighovho a Jeansovho zákona nebol správny?

3. Na základe ktorých predpokladov formuloval Planck zákon vyžarovania pre absolútne čierne teleso?

4. Porovnajte Planckov zákon vyžarovania s Rayleighovhovým a Jeansovým zákonom vyžarovania.

5. Kto je tvorcom myšlienky vyžarovania energie po kvantách?

6. Čo rozumieme pod pojmom kvantum energie?

7. Kto je tvorcom myšlienky, že energia sa šíri prostredím po kvantách?

8. Napíšte od ktorých fyzikálnych veličín závisí spektrálna hustota intenzity vyžarovania absolútne čierneho telesa.

9. Matematicky formulujte Planckov zákon žiarenia.

10. Definujte pojem Planckova redukovaná konštanta.

11. Čo vystihuje pojem „ultrafialová katastrofa“?