NEROVNOVÁŽNE SYSTÉMY
1. Riešte problém Verhulstovej evolučnej rovnice 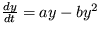 analyticky aj kvalitatívnou analýzou.
analyticky aj kvalitatívnou analýzou.
Riešenie: Analyticky: Hľadajte riešenie tejto diferenciálnej rovnice. Dostanete funkciu 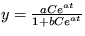 , ktorá má dve stacionárne riešenia:
, ktorá má dve stacionárne riešenia:
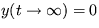 pre a<0 a
pre a<0 a 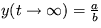 pre a>0.
pre a>0.
Kvalitatívne: Riešte pomocou metódy malých odchýlok. Dostanete stacionárne stavy:
y 1s= 0 stabilný pre a<0 a 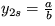 stabilný pre a>0.
stabilný pre a>0.
2. Pohybová rovnica lineárneho harmonického oscilátora 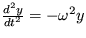 obsahuje druhú deriváciu podľa času. Riešte túto rovnicu priamo ako diferenciálnu rovnicu druhého rádu a aj pomocou rozkladu na evolučné rovnice.
obsahuje druhú deriváciu podľa času. Riešte túto rovnicu priamo ako diferenciálnu rovnicu druhého rádu a aj pomocou rozkladu na evolučné rovnice.
Riešenie: Pri priamom riešení použite ako riešenie funkciu y = Cept. Pri druhom spôsobe použite rozklad rovnice druhého rádu na systém dvoch rovníc prvého rádu 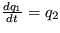 ,
, 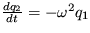 a riešte ich.
a riešte ich.
3. Určte stacionárne riešenia pohybovej rovnice lineárneho harmonického oscilátora z predchádzajúceho príkladu a vyšetrite ich stabilitu.
Riešenie: Rozkladom pohybovej rovnice na dve evolučné rovnice (príklad 2.) a zisťovaním ich stability, dostanete stacionárne riešenie ys=0, 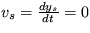 , pričom koeficient v exponente časového vývoja malých odchýliek bude
, pričom koeficient v exponente časového vývoja malých odchýliek bude 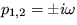 , čo je režim oscilácií okolo stabilného stredu s uhlovou frekvenciou
, čo je režim oscilácií okolo stabilného stredu s uhlovou frekvenciou 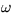 .
.
4. Pohybová rovnica tlmeného lineárneho oscilátora má tvar 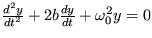 , kde b je koeficient útlmu a
, kde b je koeficient útlmu a 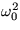 je vlastná frekvencia oscilátora. Určte stacionárny stav takéhoto oscilátora a jeho stabilitu. Výsledok interpretujte.
je vlastná frekvencia oscilátora. Určte stacionárny stav takéhoto oscilátora a jeho stabilitu. Výsledok interpretujte.
Riešenie: Stacionárny stav je ys =0, 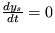 a koeficient v exponente vývoja malých odchýliek je
a koeficient v exponente vývoja malých odchýliek je 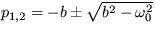 . Takže pre
. Takže pre 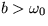 máme stabilný uzol, pre
máme stabilný uzol, pre 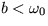 máme režim stabilného ohniska. Pri tomto režime sa jedná o tlmené oscilácie s uhlovou frekvenciou
máme režim stabilného ohniska. Pri tomto režime sa jedná o tlmené oscilácie s uhlovou frekvenciou
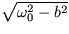 okolo stacionárnej polohy.
okolo stacionárnej polohy.
5. Máme homogénnu tyč dĺžky l a hmotnosti m, ktorá je upevnená tak, že sa môže otáčať vo vertikálnej rovine (trenie zanedbávame). Takýto systém má dve stacionárne polohy, z ktorých jedna je nestabilná a okolo druhej stacionárnej polohy pri malých odchýlkach harmonicky kmitá. Dokážte to rozborom stability evolučných rovníc tohoto systému. (Moment zotrvačnosti homogénnej tyče vzhľadom na os prechádzajúcu ťažiskom je 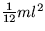 , tiažové zrýchlenie je g.)
, tiažové zrýchlenie je g.)
Riešenie: Stacionárne polohy sú dané rovnicami 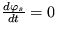 a
a 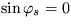 , kde
, kde 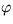 je uhol otočenia okolo osi prechádzajúcej bodom upevnenia. Z toho pre stacionárnu polohu dostanete podmienku
je uhol otočenia okolo osi prechádzajúcej bodom upevnenia. Z toho pre stacionárnu polohu dostanete podmienku 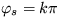 a k je celé číslo. To zodpovedá dvom stacionárnym riešeniam:
a k je celé číslo. To zodpovedá dvom stacionárnym riešeniam:
k = 0, 2, 4, ... párne - ťažisko je najnižšie a
k = 1, 3, 5, ... nepárne - ťažisko je najvyššie.
Pre k párne dostávame 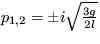 - režim oscilácií okolo stabilného stredu. Pre k nepárne je
- režim oscilácií okolo stabilného stredu. Pre k nepárne je 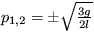 - režim nestabilného sedla.
- režim nestabilného sedla.
6. Aplikujte kvalitatívnu anlýzu na rovnicu 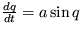 .
.
Riešenie: Stacionárne stavy 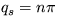 , pričom body
, pričom body 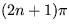 sú stabilné a body
sú stabilné a body 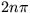 sú nestabilné.
sú nestabilné.
7. Na obrázku 1 máme systém dvoch spriahnutých oscilátorov. Každý z nich má hmotnosť m. Tuhosť krajných pružín je s a tuhosť prostrednej S. Tento systém môžeme popísať pohybovými rovnicami v tvare 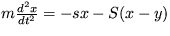 a
a 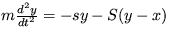 .
.
Vyšetrite stabilitu systému a určte vlastné frekvencie, s ktorými môže kmitať.
Obrázok 1:
![\begin{figure}
\begin{center}
\includegraphics [width=8.0cm]{nerovs2.eps}
\end{center}\end{figure}](img32.gif) |
Riešenie: Stacionárny stav je určený rovnicami xs=0, 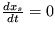 , ys=0 a
, ys=0 a 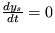 . Pre exponenciálny faktor časového vývoja porúch dostanete
. Pre exponenciálny faktor časového vývoja porúch dostanete 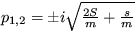 a
a 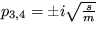 - jedná sa o režim oscilácií okolo stabilného stredu. Pre vlastné frekvencie systému (frekvencie módov) z toho vychádza
- jedná sa o režim oscilácií okolo stabilného stredu. Pre vlastné frekvencie systému (frekvencie módov) z toho vychádza 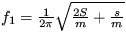 a
a 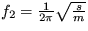 .
.
8. Teleso hmotnosti m s kladným elektrickým nábojom e sa pohybuje vplyvom potenciálu 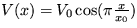 . Nájdite stacionárne polohy a určte ich stabilitu.
. Nájdite stacionárne polohy a určte ich stabilitu.
Riešenie: Stacionárne polohy sú dané podmienkami xs=kx0, 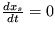 . Pre koeficient v exponente časového vývoja odchýlok platí
. Pre koeficient v exponente časového vývoja odchýlok platí 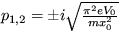 - režim oscilácií okolo stabilného stredu pre nepárne hodnoty k a
- režim oscilácií okolo stabilného stredu pre nepárne hodnoty k a 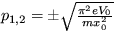 - režim nestabilného sedla pre párne hodnoty k. Môžete si vyskúsať rovnakú úlohu s potenciálom
- režim nestabilného sedla pre párne hodnoty k. Môžete si vyskúsať rovnakú úlohu s potenciálom 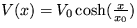
9. Evolučná rovnica pre veľryby má v prvom priblížení tvar 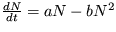 . Koľko veľrýb je možné ročne uloviť, aby nevyhynuli?
. Koľko veľrýb je možné ročne uloviť, aby nevyhynuli?
Riešenie: Evolučnú rovnicu prepíšte do tvaru 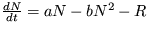 , kde R je pocet veľrýb vylovených za jednotku času. Ďalej postupujte metódou malých odchýliek a zistíte, že aby nevyhynuli, musí byť splnená podmienka
, kde R je pocet veľrýb vylovených za jednotku času. Ďalej postupujte metódou malých odchýliek a zistíte, že aby nevyhynuli, musí byť splnená podmienka 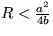 a stacionárne stabilné riešenie je
a stacionárne stabilné riešenie je 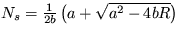 .
.
10. Predpokladajme, že systém rysov a zajacov je popísaný Voltterovými-Lotkovými rovnicami:
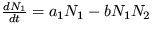 - zajace,
- zajace,
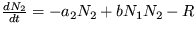 - rysy.
- rysy.
Koľko rysov R treba odstreliť, aby tento systém neosciloval?
Riešenie: Stabilný režim je možný len s podmienkou R<0, takže rysy nie je možné strieľať, ale bolo by ich treba pridávať.
11. Dokážte, že systém popísaný rovnicami:
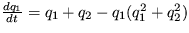 ,
,
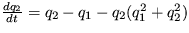 ,
,
vykazuje oscilácie v limitnom cykle.
Riešenie: Ukážte, že systém je v režime nestabilného ohniska. Takže ak by aj bol systém v stacionárnom stave (bod vo fázovom priestore), už pri malej fluktuácii sa začne pohybovať po špirále od tohoto stacionárneho bodu. Bolo by treba ešte ukázať, že tento pohyb je ohraničený, takže systém naozaj skončí v režime limitného cyklu a nedôjde k jeho deštrukcii. K tomu už ale naše jednoduché prostriedky nestačia.
Pri vhodnej voľbe 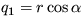 ,
, 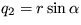 môžete dané rovnice analyticky riešiť a dostanete riešenie
môžete dané rovnice analyticky riešiť a dostanete riešenie 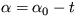 ,
, 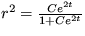 , čo naozaj je režim limitného cyklu.
, čo naozaj je režim limitného cyklu.
Obrázok 2:
![\begin{figure}
\begin{center}
\includegraphics [width=9cm]{nerovs1.eps}
\end{center}\end{figure}](img54.gif) |
12. Pod dlhou horizontálnou vodivou traverzou visí na dvoch rovnakých pružinách s tuhosťou k priamy drôt dĺžky L (obr. 2). Ak traverzou a drôtom neprechádza elektrický prúd, je medzi nimi vzdialenosť h. V akej vzdialenosti x sa drôt ustáli, ak traverzou začne prechádzať prúd I1 a drôtom prúd I2 toho istého smeru? Aká bude stabilita riešenia?
Riešenie: Prepíšte pohybovú rovnicu pre zavesený drôt na dve evolučné rovnice a hľadajte ich stacionárne riešenia a vyšetrite ich stabilitu. Stacionárne riešenia dostanete v tvare 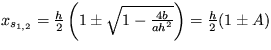 , a
, a 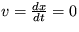 , pričom platí:
, pričom platí: 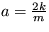 a
a 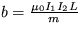 . Z podmienky
. Z podmienky 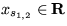 vidíte, že
vidíte, že 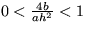 a teda 0<A<1. Pre koeficient v časovej závislosti výchyliek zo stacionárnych polôh dostanete
a teda 0<A<1. Pre koeficient v časovej závislosti výchyliek zo stacionárnych polôh dostanete 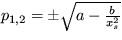 . Z podmienky pre stacionárne riešenie axs2 -ahxs+b=0 vyjadríte
. Z podmienky pre stacionárne riešenie axs2 -ahxs+b=0 vyjadríte 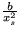 a dosadíte do vzťahu pre p1,2. Dostanete nakoniec
a dosadíte do vzťahu pre p1,2. Dostanete nakoniec 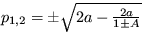 . Pre riešenie
. Pre riešenie 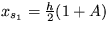 bude
bude 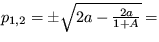
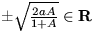 , takže toto stacionárne riešenie je v režime nestabilného sedla. Pre druhé riešenie
, takže toto stacionárne riešenie je v režime nestabilného sedla. Pre druhé riešenie 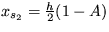 bude
bude 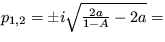
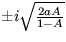 , takže je v režime oscilácií okolo stabilného stredu. Uhlová frekvencia týchto oscilácií je
, takže je v režime oscilácií okolo stabilného stredu. Uhlová frekvencia týchto oscilácií je 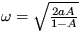 .
.
13. Dokážte, že Van der Pohlov oscilátor s pohybovou rovnicou 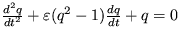 môže vykazovať oscilácie v režime limitného cyklu.
môže vykazovať oscilácie v režime limitného cyklu.
Riešenie: Pohybovú rovnicu prevediete na systém dvoch evolučných rovníc: 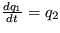 a
a 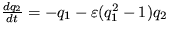 , a ukážete, že môžu byť v režime nestabilného ohniska pre
, a ukážete, že môžu byť v režime nestabilného ohniska pre 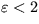 .
.
14. Zaveďte takú reguláciu do Voltterových-Lotkových systémov, aby po porušení stacionárneho stavu neoscilovali. Využite pritom výsledok príkladu 10.
Riešenie: Voltterove-Lotkove rovnice prepíšte do tvaru
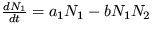 a
a
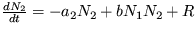 ,
,
a postupujte metódou malých odchýliek. Obe premenné sú nenulové pri stacionárnom riešení 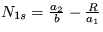 a
a 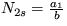 . Pre koeficienty v exponentách malých výchyliek dostanete
. Pre koeficienty v exponentách malých výchyliek dostanete 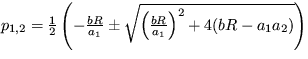 . Podmienku pre stabilný režim bez oscilácií môžete písať v tvare
. Podmienku pre stabilný režim bez oscilácií môžete písať v tvare 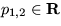 a p1,2<0, z čoho pre R dostanete
a p1,2<0, z čoho pre R dostanete 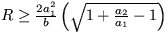 a súčasne
a súčasne 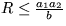 .
.
15. Dokážte, že trojzložkový systém môže vykazovať desať rozličných režimov činnosti.
Riešenie: Uvažujte evolučné rovnice trojzložkového systému v nasledujúcom tvare:
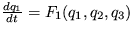 ,
, 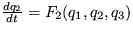 a
a 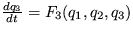 .
.
Analyzujte stabilitu riešení tohoto systému. To vedie na rovnicu tretieho rádu pre koeficienty v exponentách odchýlok od stacionárnych riešení a z toho automaticky dostanete hľadaných desať režimov.
16. Jednoduchý dvojzložkový symbiotický systém sa dá popísať evolučnými rovnicami:
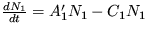 ,
,
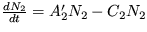 ,
,
pričom pre koeficienty A'1, A'2 platí A'1=A1+B1N2 a A'2=A2+B2N1. V tejto závislosti je možné vidieť princíp symbiózy. Ak totiž pribúda jedincov N1, zvačšuje sa koeficient A'2 a zvačšuje sa aj počet jedincov druhého druhu N2. A platí to samozrejme aj opačne. Vyšetrite stabilitu stacionárnych riešení takéhoto symbiotického systému.
Riešenie: Okrem triviálneho nulového riešenie získate metódou malých odchýliek riešenie 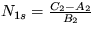 a
a 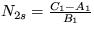 . Pre exponentu v odchýlkach malých riešení dostanete potom
. Pre exponentu v odchýlkach malých riešení dostanete potom 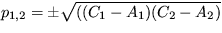 , z čoho vidíte, že takýto symbiotický systém je v režime nestabilného sedla.
, z čoho vidíte, že takýto symbiotický systém je v režime nestabilného sedla.
17. Dokážte, že aj bez použitia otrockého princípu, sa dá nájsť bifurkačný bod pre laser.
Riešenie: Vychádzajte z evolučných rovníc pre laser
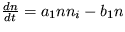 ,
, 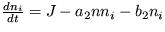 .
.
Dostanete dva možné stacionárne stavy:
nsa=0 a 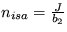 ,
, 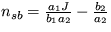 a
a 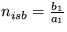 .
.
Z požiadavky, aby bol v laseri nenulový počet fotónov n>0, dostaneme pre plnenie, pri ktorom nastáva vynútená emisia, podmienku 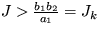 , kde Jk je kritická hodnota plnenia. Analýzou stability prvého stacionárneho riešenia zasa zistíte, že pre J<Jk je toto prvé riešenie stabilné. Takže pri kritickej hodnote plnenia Jk dochádza pri lasery k bifurkácii - zmení sa režim činnosti.
, kde Jk je kritická hodnota plnenia. Analýzou stability prvého stacionárneho riešenia zasa zistíte, že pre J<Jk je toto prvé riešenie stabilné. Takže pri kritickej hodnote plnenia Jk dochádza pri lasery k bifurkácii - zmení sa režim činnosti.
18. Dokážte, že pri konštantnej záťaži, môže Van der Pohlov oscilátor vykonávať kmity (v režime limitného cyklu) okolo vysunutej stacionárnej polohy (analógia s mostom, ktorý je vystavený horizontálnej záťaži).Uvažujte jednorozmerný prípad, pri ktorom dodatočná konštantná sila pôsobí v smere osi x.
Riešenie: Pohybovú rovnicu pre Van der Pohlov oscilátor v tomto prípade môžete písať ako 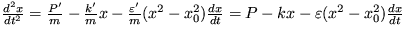 . P' je pôsobiaca sila. Po prepísaní tejto rovnice na sústavu dvoch evolučných rovníc vyšterite stabilitu riešení a dostanete, že stacionárny stav je
. P' je pôsobiaca sila. Po prepísaní tejto rovnice na sústavu dvoch evolučných rovníc vyšterite stabilitu riešení a dostanete, že stacionárny stav je 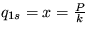 a
a 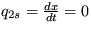 . Riešenie bude oscilovať ak
. Riešenie bude oscilovať ak 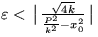 . Ak P>kx0 budú tieto oscilácie tlmené. Ak P<kx0 budú riešením oscilácie v režime limitného cyklu.
. Ak P>kx0 budú tieto oscilácie tlmené. Ak P<kx0 budú riešením oscilácie v režime limitného cyklu.
19. Plazma v polovodiči je opísaná evolučnými rovnicami
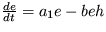 ,
,
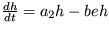 ,
,
kde e a h je koncentrácia elektrónov a dier a a1, a2, b sú kladné konštanty. V akom režime bude tento systém v stacionárnom stave?
Riešenie: Pomocou kvalitatívnej analýzy dostanete dve stacionárne riešenia esa = 0, hsa = 0 a 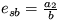 ,
, 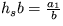 . Prvé riešenie je v režime nestabilného uzla (p1=a1 a p2=a2) a druhé riešenie je v režime nestabilného sedla (
. Prvé riešenie je v režime nestabilného uzla (p1=a1 a p2=a2) a druhé riešenie je v režime nestabilného sedla (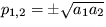 ).
).
20. Nájdite podmienky stability riešenia systému opísaného evolučnou rovnicou
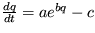 .
.
Riešenie: Stacionárne riešenie 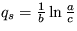 je stabilné len ak sú rozdielne znamienka koeficientov b a c.
je stabilné len ak sú rozdielne znamienka koeficientov b a c.
21. Pohybovú rovnicu pre pohyb telesa hmotnosti m v gravitačnom poli telesa hmotnosti M (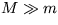 ) v n rozmernom priestore môžeme napísať v tvare
) v n rozmernom priestore môžeme napísať v tvare
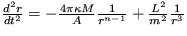 ,
,
kde A je konštanta a L je moment hybnosti telesa m. Ukážte, že pre rozmer priestoru 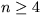 nedostaneme pre tento problém oscilujúce riešenia.
nedostaneme pre tento problém oscilujúce riešenia.
Riešenie: Pre koeficienty v časovom rozvoji porúch dostanete pomocou kvalitatívnej analýzy vzťah 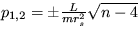 , v ktorom rs je stacionárna hodnota polomeru r. Koeficienty p1,2 budú mať komplexné hodnoty len pre n<4.
, v ktorom rs je stacionárna hodnota polomeru r. Koeficienty p1,2 budú mať komplexné hodnoty len pre n<4.
22. Interakcia dvoch sociálnych táborov je opísaná sústavou evolučných rovníc:
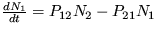 ,
,
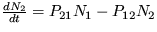 ,
,
pričom N1+N2=N a pre koeficienty platí P12 = const a 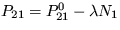 . Určte podmienku na existenciu stacionárneho riešenia.
. Určte podmienku na existenciu stacionárneho riešenia.
Riešenie: Stabilné riešenie existuje len pre hodnotu 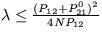 .
.
23. Evolučná rovnica pre povrchovú teplotu Zeme T v interakcii so slnečným žiarením má tvar
![$C \frac {dT}{dt}= \frac Q4 [1-\alpha(T)]-\varepsilon \sigma T^4$](img114.gif) ,
,
kde C je renormalizovaná tepelná kapacita Zeme, Q je solárna konštanta (1360 W/m2), 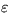 je koeficient charakterizujúci odchýlku tepelného vyžarovania Zeme od čierneho telesa (0,61) a
je koeficient charakterizujúci odchýlku tepelného vyžarovania Zeme od čierneho telesa (0,61) a 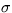 je Stefanova-Boltzmannova konštanta. Funkcia
je Stefanova-Boltzmannova konštanta. Funkcia 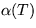 je daná vzťahom
je daná vzťahom 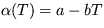 , pričom a=2,75 a b=0.0085. Určte stacionárne stavy a preskúmajte ich stabilitu.
, pričom a=2,75 a b=0.0085. Určte stacionárne stavy a preskúmajte ich stabilitu.
Riešenie: Stacionárne stavy, určené pomocou počítača, vychádzajú T1=259,4 K a T2=293,0 K. Prvé riešenie je nestabilné, druhé stabilné.
24. Vzťah medzi teplotou oceánu a množstvom ľadu v ňom je v renormalizovaných súradniciam daný systémom rovníc
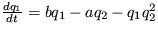 ,
,
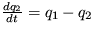 .
.
Určte podmienky existencie stacionárneho stavu a jeho stabilitu.
Riešenie: Z podmienky existencie nenulového reálneho stacionárneho stavu dostanete pre hodnoty koeficientov a, b nerovnosť b > a. Aby bol tento stav aj stabilný (režim stabilného uzla) musí byť navyše splnená podmienka a<1.
25. Nájdite evolučné rovnice kovového drôtu v žiarovke, ktorou prechádza elektrický prúd a stanovte podmienky stabilného režimu.(Predpokladajte, že poznáte priemer drôtu d, jeho merný odpor 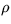 pri teplote okolia T0 a teplotný koeficient odporu
pri teplote okolia T0 a teplotný koeficient odporu 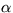 .)
.)
Riešenie: Uvažujte elektrický výkon, ktorým sa drôt zahrieva, stratu tepla ohrievaním a stratu tepla vyžarovaním. Nezabudnite na zmenu odporu s teplotou. Evolučná rovnica napokon bude ![$C\frac {dT}{dt}= \frac {4\rho l}{\pi d^2}I^2[1+\alpha(T-T_0)]-\pi dl \sigma (T^4-T_0^4)$](img123.gif) , kde C je tepelná kapacita a l je dĺžka drôtu. Stacionárne stavy je možné pre konkrétnu hodnotu prúdu určtiť pomocou počítača. Analýzou stability riešení dostaneme podmienku pre prúd
, kde C je tepelná kapacita a l je dĺžka drôtu. Stacionárne stavy je možné pre konkrétnu hodnotu prúdu určtiť pomocou počítača. Analýzou stability riešení dostaneme podmienku pre prúd 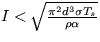 .
.
26. Ukážte, že pre vznik priestorovej štrukturalizácie by (teoreticky) stačilo
predpokladať, že rýchlosť presunu sa mení.
Riešenie: Vychádzajte z evolučnej rovnice
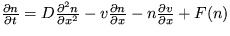 ,
,
pričom predpokladajte nulovú pôsobiacu silu a závislosť rýchlosti v=v0(1-ax). Analýzou stability stacionárneho riešenia, za predpokladu, že koeficient k, charakterizujúci priestorový vývoj fluktuácií, musí byť komplexný, dostanete podmienku 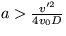 , kde v' je hodnota rýchlosti v bode, v ktorom vzniká štrukturalizácia.
, kde v' je hodnota rýchlosti v bode, v ktorom vzniká štrukturalizácia.
27. Aplikujte kvalitatívnu analýzu na trojparametrický Lorentzov (klimatický) systém, ktoý je daný trojicou evolučných rovníc
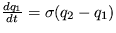 ,
,
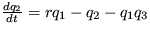 ,
,
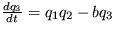 .
.
Riešenie: Systém má tri rôzne stacionárne riešenia:
q1sa=q2sa=q3sa=0, 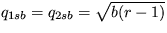 , q3sb=r-1 a
, q3sb=r-1 a 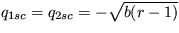 , q3sc=r-1. Prvé riešenie je stabilné ak b>0 a r<1, stabilitu ostatných riešení je možné určiť pomocou počítača.
, q3sc=r-1. Prvé riešenie je stabilné ak b>0 a r<1, stabilitu ostatných riešení je možné určiť pomocou počítača.
28. Cievka, napájaná prúdom I, sa chladí médiom s teplotou T0 tak, že odvod tepla z jej povrchu sa odohráva podľa Newtonovho zákona a pre teplo odobraté z cievky za čas dt môžete písať dQ=KS(T-T0)dt, kde K je koeficient prestupu tepla a S je obsah povrchu cievky. Určte kritický prúd, ktorý môže cievkou prechádzať, ak teplota topenia drôtu, z ktorého je cievka zhotovená, je TT, jeho teplotný koeficient odporu je 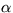 a odpor drôtu pri teplote T0 je R0.
a odpor drôtu pri teplote T0 je R0.
Riešenie: Pre kritický prúd dostanete vzťah ![$I_K=\sqrt{\frac{KS(T_T-T_0)}{R_0[1+\alpha(T_T-T_0)]}}$](img132.gif) .
.
29. Prepíšte Volterove-Lotkove rovnice, Selkovove rovnice pre glykolýzu a rovnice pre fotosyntézu do diskrétnej podoby.
Riešenie: Využite transformácie 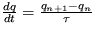 .
.
30. Ukážte, že už na molekulárnej úrovni je prítomná selekcia. Uvažujte vzájomné reakcie troch látok s koncentráciami n0, n1 a n2, ktoré sú popísané systémom evolučných rovníc
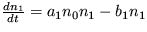 ,
,
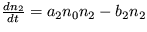 ,
,
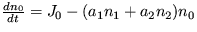 ,
,
kde a1, a2, b1 a b2 sú kladné konštanty a J0 je konštantný prítok látky n0.
Riešenie: Dostanete dve stacionárne riešenia n1sa=0, 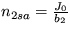 ,
, 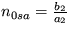 a
a 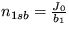 , n2sb=0,
, n2sb=0, 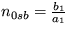 . Prvé riešenie je stabilné keď
. Prvé riešenie je stabilné keď 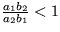 , druhé je stabilné keď
, druhé je stabilné keď 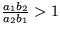 . čiže podľa konkrétnych hodnôt koeficientov a a b bude prevládať buď prvá alebo druhá látka.
. čiže podľa konkrétnych hodnôt koeficientov a a b bude prevládať buď prvá alebo druhá látka.
31. Evolučná rovnica fotoelektrónov v polovodiči má tvar 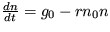 , kde g0 a n0 sú konštanty. Aká je stacionárna hodnota koncentrácie elektrónov n v zašumenom prostredí, kde koeficient r fluktuuje podľa vzťahu
, kde g0 a n0 sú konštanty. Aká je stacionárna hodnota koncentrácie elektrónov n v zašumenom prostredí, kde koeficient r fluktuuje podľa vzťahu 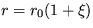 ? (Ide o biely šum.)
? (Ide o biely šum.)
Riešenie: Vychádzajte z Itovej rovnice. Ak v zašumenom prostredí platí evolučná rovnica 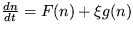 , pre stacionárny stav dostanete podmienku
, pre stacionárny stav dostanete podmienku 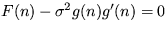 .V našom prípade dostanete stacionárnu koncentráciu
.V našom prípade dostanete stacionárnu koncentráciu 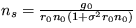 .
.
32. Guľôčka sa pohybuje vo viskóznom prostredí, pričom jej rýchlosť je opísaná rovnicou 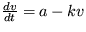 . Aká je stacionárna hodnota rýchlosti, ak koeficient k fluktuuje podľa vzťahu
. Aká je stacionárna hodnota rýchlosti, ak koeficient k fluktuuje podľa vzťahu 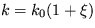 ?
?
Riešenie: Treba vychádzať z Itovej rovnice. Stacionárna hodnota rýchlosti bude 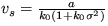 .
.
33. Obvod istého územia bol použitím meracieho pásu dĺžky 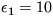 m určený na l1= 10 km. Akú dĺžku l2 by sme namerali pri použití pásma dĺžky
m určený na l1= 10 km. Akú dĺžku l2 by sme namerali pri použití pásma dĺžky 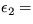 2 m, ak fraktálová dimenzia hranice daného územia je D=1,2?
2 m, ak fraktálová dimenzia hranice daného územia je D=1,2?
Riešenie: Využitím vzťahu pre fraktálovú dimenziu dostanete rovnosť 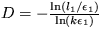 a
a 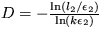 . Konštanta k vystupuje vo vzťahu preto, lebo ten platí presne len v limite
. Konštanta k vystupuje vo vzťahu preto, lebo ten platí presne len v limite 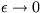 . Vďaka tejto konštante navyše dosiahneme, že v logaritmoch v menovateli bude bozrozmerný výraz. Po eliminovaní k dostanete vzťah
. Vďaka tejto konštante navyše dosiahneme, že v logaritmoch v menovateli bude bozrozmerný výraz. Po eliminovaní k dostanete vzťah 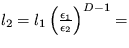 13,8 km.
13,8 km.
34. Nájdite základný nenulový stav a určte jeho stabilitu pre systém opísaný logistickou rovnicou 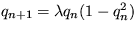 . Predpokladajte, že
. Predpokladajte, že 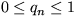 .
.
Riešenie: Stacionárny stav 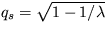 je stabilný pre parameter
je stabilný pre parameter 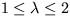 .
.
Dokument bol vygenerovaný programom latex2html 16. 5. 2002.
![\begin{figure}
\begin{center}
\includegraphics [width=8.0cm]{nerovs2.eps}
\end{center}\end{figure}](img32.gif)
![\begin{figure}
\begin{center}
\includegraphics [width=9cm]{nerovs1.eps}
\end{center}\end{figure}](img54.gif)
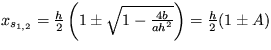 , a
, a 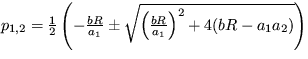 . Podmienku pre stabilný režim bez oscilácií môžete písať v tvare
. Podmienku pre stabilný režim bez oscilácií môžete písať v tvare