

Up: Zoznam tém
Previous: Elektromagnetická indukcia
GRAVITAČNÉ POLE
1. Dve medené gule s polomermi r1 = 2 cm, r2 = 3 cm, sa
dotýkajú. Aká je gravitačná potenciálna energia
tejto sústavy ? (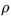 = 8,6.103 kg/m3)
= 8,6.103 kg/m3)
[ 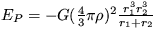 = -3,74.10-10 J (G je gravitačná konštanta)]
= -3,74.10-10 J (G je gravitačná konštanta)]
2 V kovovej homogénnej guli s polomerom R je vytvorená
dutina s polomerom r = R/2 (obr.). Hmotnosť tejto gule bez dutiny
je M . Akou veľkou silou pôsobí toto teleso na malú
guľôčku hmotnosti m , ktorej stred leží na osi
symetrie telesa a je od stredu pôvodnej gule vzdialený o
dĺžku d ?
[ ![$F = GmM[\frac{1}{d^2}-\frac{1}{8(d-R/2)^2}]$](img3.gif) ]
]
![\begin{figure}
\centering
\includegraphics [width=0.5\textwidth]{GravPole_obr02.eps}
\end{figure}](img4.gif)
3. Akou veľkou gravitačnou silou pôsobí
homogénny drôt hmotnosti m ohnutý do tvaru kružnice s
polomerom R na hmotný bod s hmotnosťou M ležiaci na osi
kružnice vo vzdialenosti a od jej stredu ?
[ 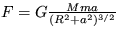 ]
]
![\begin{figure}
\centering
\includegraphics [width=0.5\textwidth]{GravPole_obr03.eps}
\end{figure}](img6.gif)
4. Vypočítajte potenciál a intenzitu
gravitačného poľa homogénneho drôtu hmotnosti m
ohnutého do tvaru kružnice s polomerom R v bode P na osi
kružnice vo vzdialenosti a od jej stredu.
[ 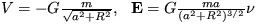 , kde
, kde 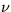 je jednotkový
vektor kolmý na rovinu drôtu a orientovaný ku drôtu. ]
je jednotkový
vektor kolmý na rovinu drôtu a orientovaný ku drôtu. ]
5. Určte veľkosť gravitačného
zrýchlenia g ako funkciu vzdialenosti h od zemského povrchu,
keď poznáte polomer Zeme R a zrýchlenie g0 na povrchu Zeme.
[ 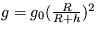 ]
]
6. V akej vzdialenosti od povrchu Zeme má
gravitačné zrýchlenie veľkosť 1 m/s2 , keď
polomer Zeme R = 6378 km a na povrchu Zeme g0 = 9,81 m/s2 .
[ 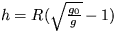 = 13598,5 km ]
= 13598,5 km ]
7. Typická neutrónová hviezda má hmotnosť
Slnka (m = 2.1030 kg) , ale polomer len R = 10 km.
Vypočítajte
a) aké je gravitačné zrýchlenie na povrchu hviezdy,
b) akú rýchlosť získa voľne padajúce teleso na
dráhe dĺžky s = 1 m .
[ a) g = Gm/R2 = 13,34.1011 m/s2, b) 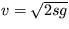 =
1,633.106 m/s ]
=
1,633.106 m/s ]
8. V akom vzťahu je výška veže H s hĺbkou
šachty h , keď na vrchole veže a na dne šachty je doba
kmitu toho istého matematického kyvadla rovnaká ? Polomer
Zeme 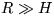 .
.
[ 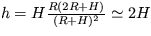 ]
]
9. Nájdite zrýchlenie, ktorým by padali telesá
na povrchu Mesiaca ak predpokladáme, že na telesá
pôsobí len gravitačné pole Mesiaca a keď vieme,
že medzi hmotnosťami a polomermi Mesiaca a Zeme platia
vzťahy 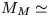 1/81 MZ ,
1/81 MZ , 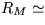 1/4 RZ .
1/4 RZ .
[ 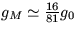 = 1.938 ms-2 ]
= 1.938 ms-2 ]
10. Nájdite hodnotu rýchlosti v0 , ktorú treba
udeliť v smere zvislom nahor telesu nachádzajúcemu sa na
povrchu Zeme, aby sa dostalo do výšky h = RZ . Odpor prostredia
neuvažujte, RZ = 6370 km .
[ 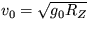 = 7,905 km/s ]
= 7,905 km/s ]
11. Akú rýchlosť treba udeliť rakete
nachádzajúcej sa na povrchu Zeme, aby sa vymanila z jej
gravitačného poľa ? ( R = 6378 km, g0 = 9,81 m/s2 ).
[ 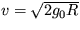 = 11,2 km/s ]
= 11,2 km/s ]
12. Ak skokan vyskočí na povrchu Zeme do výšky
hZ = 1,2 m , do akej výšky hM vyskočí na Mesiaci, ak
pri odraze vyvinie rovnaký impulz ako na Zemi ? Hmotnosť a
polomer Mesiaca: MM = 6,7.1022 kg , RM = 1,6.106 m .
[ 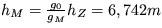 ]
]
13. Teleso s hmotnosťou m sa nachádza najprv na povrchu
Zeme, potom vo výške h nad jej povrchom (hmotnosť Zeme M a
jej polomer R sú známe). Určte
a) rozdiel potenciálnej energie 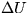 telesa vo výške
h a na
povrchu Zeme, t.j. potenciálnu energiu vzhľadom na povrch Zeme,
telesa vo výške
h a na
povrchu Zeme, t.j. potenciálnu energiu vzhľadom na povrch Zeme,
b) 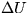 pre
pre 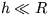 .
.
[ a) 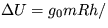 , kde g0 = GM/R2, b)
, kde g0 = GM/R2, b) 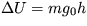 ]
]
14. Vypočítajte, v ktorom mieste na spojnici medzi
Zemou a Mesiacom sa intenzita ich spoločného
gravitačného poľa rovná nule ! Hmotnosť Mesiaca
MM = 1/81 MZ , vzdialenosť stredov oboch telies 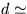 380 000 km .
380 000 km .
[ x = 0,9 d = 342 000 km od stredu Zeme ]
15. Telesu s hmotnosťou m , ktoré sa nachádza na
povrchu Zeme , udelíme vo vertikálnom smere
rýchlosť v0 . Akú výšku h teleso dosiahne, ak
v0 je
menšie než 2. kozmická rýchlosť ? Odpor prostredia
neuvažujte.
[ h = v0 2R/(2g0R-v0 2) ]
16. Teleso padá voľným pádom z veľkej
výšky 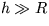 (R je polomer Zeme). Akou rýchlosťou
v0
by dopadlo na Zem, ak by sa pohybovalo vo vákuu ?
(R je polomer Zeme). Akou rýchlosťou
v0
by dopadlo na Zem, ak by sa pohybovalo vo vákuu ?
[ 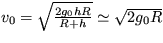 ]
]
17. Určte obvodovú rýchlosť, ktorou Zem obieha
okolo Slnka, za predpokladu, že dráha Zeme je kruhová s
polomerom Rd = 1,5.108 km, a keď vieme, že hmotnosť
Slnka MS = 2.1030 kg.
[ v = 29,82 km/s ]
18. Dokážte, že úniková rýchlosť
v2 od Slnka na kružnici po ktorej sa pohybuje Zem je 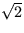 krát
väčšia než obežná rýchlosť v1 Zeme
okolo Slnka.
krát
väčšia než obežná rýchlosť v1 Zeme
okolo Slnka.
[ 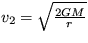
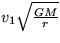 ]
]
19. Vypočítajte hmotnosť Slnka MS ak
predpokladáme, že Zem obieha po kruhovej dráhe s polomerom
R = 149 504 200 km a dobou obehu T = 365,25 dní. Pomocou
známeho polomeru Slnka RS = 695 300 km potom vypočítajte
tiažové zrýchlenie gS na jeho povrchu.
[ MS = 1,986.1030, gS = 274 m/s2 ]
20. Vzdialenosť Marsu od Slnka je 1,52-krát
väčšia ako vzdialenosť Zeme od
Slnka. Na základe tohto údaja určte obežnú dobu
Marsu okolo Slnka.
[ TM = 1,874 TZ = 684 dní ]
21. Umelá družica obieha okolo Zeme po kruhovej
dráhe vo výške 200 km nad zemským povrchom. Určte
jej obvodovú rýchlosť v0 a dobu jedného obehu T .
Polomer Zeme R = 6378 km.
[ 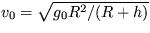 7,79 km/s,
7,79 km/s, 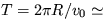 1,43 h ]
1,43 h ]
22. Určte dostredivé zrýchlenie družice pri
jej pohybe po kruhovej dráhe okolo Zeme vo výške h = 200 km nad
jej povrchom. Polomer Zeme R = 6378 km .
[ ad = g0[R/(R+h)]2 = 9,22 m/s2 ]
23. V akej vzdialenosti h od povrchu Zeme sa nachádza
stacionárna družica, ktorá sa pohybuje po kruhovej
dráhe v rovine rovníka ? Polomer Zeme R = 6378 km, g0 =
9,81 ms-2 , uhlová rýchlosť Zeme 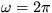 /deň.
/deň.
[ ![$h = \sqrt[3]{g_0R^2/\omega ^2} - R \simeq$](img33.gif) 36 000 km ]
36 000 km ]
24. Ak by stredom Zeme pozdĺž jej priemeru
prechádzal tunel, ukážte, že sila pôsobiaca na
teleso hmotnosti m , ktoré z povrchu Zeme voľne pustíme do
tunela, je priamo úmerná jeho vzdialenosti x od stredu Zeme a
smeruje do jej stredu (obr.) Polomer Zeme R = 6378 km, g0 = 9,81
ms-2. Ďalej vypočítajte čas t1 , za ktorý sa
toto
teleso dostane do stredu Zeme, čas t2 , za ktorý prejde
celým tunelom, a rýchlosť v1, ktorú má teleso v
strede tunela.
[ f = g0mx/R, 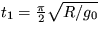 = 21,2 min.,
t2 = 2 t1 = 42,2 min,
= 21,2 min.,
t2 = 2 t1 = 42,2 min, 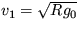 = 7,91 km/s ]
= 7,91 km/s ]
![\begin{figure}
\centering
\includegraphics [width=0.5\textwidth]{GravPole_obr24.eps}
\end{figure}](img36.gif)

Up: Zoznam tém
Previous: Elektromagnetická indukcia
Katedra fyziky FEI STU
8. 2. 2002

![\begin{figure}
\centering
\includegraphics [width=0.5\textwidth]{GravPole_obr02.eps}
\end{figure}](img4.gif)
![\begin{figure}
\centering
\includegraphics [width=0.5\textwidth]{GravPole_obr03.eps}
\end{figure}](img6.gif)
![\begin{figure}
\centering
\includegraphics [width=0.5\textwidth]{GravPole_obr24.eps}
\end{figure}](img36.gif)