8.3 Elektrostatické pole v dielektriku

Pripomeňme si, že dielektrikum je nevodivé prostredie, zložené z elektricky nabitých častíc, ktorých náboje sú navzájom vykompenzované, ale tieto náboje nie sú voľné.

Potrebné vedomosti

Pochopenie tejto kapitoly, vyžaduje poznať pojmy z elektrostatiky, ako je Coulombova sila, intenzita elektrického poľa, potenciál. Mať základné predstavy o štruktúre látky.

Učebné ciele

Študent by mal vedieť vysvetliť vlastnosti dielektrika jav polarizácie dielektrika zo štruktúry dielektrika. Mal by vedieť definovať základné veličiny charakterizujúce vlastnosti dielektrika, permitivitu, elektrickú susceptibilitu, vektor elektrickej indukcie

Kľúčové slová

dielektrikum, elektrický dipól, polarizácia, elektrická susceptibilita, elektrická indukcia,

8.3.1 Sily medzi nabitými telesami v dielektriku

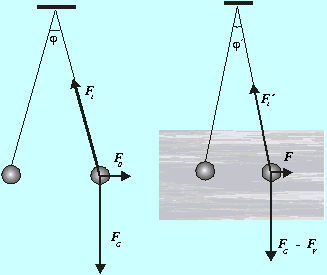
Obr. 8.3.1.1

Elektrické pôsobenie nabitých guličiek vo vákuu a dielektriku

Urobme jednoduchý pokus. Dve malé nabité vodivé guličky zavesme v jednom bode na dlhé nite (Obr.8.3.1.1). V rovnovážnom stave je nastolená rovnováha síl pôsobiacich na každú z guličiek: sily tiažovej F_g, ťažnej F_t a elektrickej F₀. Z uhla rozstupu nití j možno uvažovať o veľkosti elektrickej sily. Vložme teraz pri nezmenenom náboji guličky do dielektrického prostredia, napr. do oleja. Aj keď uvážime, že výsledná sila v zvislom smere poklesla o vztlakovú silu, zmenu uhla j sa dá vysvetliť len tak, že v dielektriku voľné náboje (nabité malé guličky) na seba pôsobia inými, menšími silami F. Ak označíme intenzitu elektrického poľa vytvoreného v svojom okolí nábojmi E₀, a intenzitu poľa v dielektriku E, potom z jej definície vyplýva, že poklesla rovnako ako elektrická sila. Táto zmena bude závisieť od voľby dielektrika. Ak zavedieme konštantu e_r , ktorá charakterizuje dielektrikum a jej význam popíšeme ďalej, potom platí:

. (8.3.1.1)

Túto zmenu možno vysvetliť len ak si bližšie rozoberieme štruktúru, elektrické vlastnosti dielektrika.

8.3.2 Dipól vo vonkajšom elektrickom poli

V homogénnom elektrickom poli pôsobí na elektrický dipól dvojica síl, ktorej moment sa dá podľa obr. 8.3.2.1 vyjadriť vektorovým súčinom

Obr. 8.3.2.1

Elektrický dipól v homogénnom elektrickom poli

, (8.3.2.1)

kde Q je kladný náboj elektrického dipólu, l je polohový vektor kladného náboja vzhľadom na záporný náboj a E je intenzita vonkajšieho homogénneho elektrického poľa, p je elektrický moment dipólu. Elektrické pole stáča elektrický dipól tak, aby jeho moment nadobudol smer elektrického poľa. Stabilný je stav, keď elektrický moment dipólu je súhlasne orientovaný s intenzitou elektrického poľa: Postavenie dipólu v orientácii opačnej k elektrickému poľu predstavuje labilnú polohu, z ktorej už malým pootočením sa voľný dipól preklápa do polohy stabilnej.

Elementárna práca dA elektrického poľa pri jeho pootočení o uhol dj je daná vzťahom

a celková práca pri preklopení dipólu z labilnej do stabilnej polohy

.

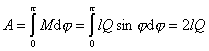Túto práca vykoná pole napr. pri otočení dipólu v striedavom elektrickom poli.

Elektrický dipól, ktorý tvoria náboje pružne viazané, okrem zmeny orientácie p stáčaním do smeru poľa, mení i svoju veľkosť zmenou dĺžky l.

8.3.3 Polarizácia dielektrika

V časti (8.2.2) bolo ukázané, že voľný náboj sídli na povrchu vodiča, to znamená na rozhraní medzi vodičom a nevodičom. Elektricky nevodivé látky - izolanty alebo dielektriká - obsahujú rovnako ako vodiče veľké množstvo nabitých častíc, v prevažnej miere sú to však len neutrálne molekuly s rovnako veľkými nábojmi s opačným znamienkom, pole od ktorých sa v makroskopickom objeme ruší. Platí to ale len pri rovnomernom rozložení nábojov. Dielektriká sa javia ako elektricky neutrálne.

Treba poznamenať, že dielektriká obsahujú tiež malý počet nabitých častíc, ktoré sa môžu v látke voľne pohybovať. Tieto náboje podmieňujú mizivo malú vodivosť izolantov, na ktorú nebudeme v ďalšom prihliadať. Aj najmenšie častice tuhých látok môžu vplyvom deformujúcich síl meniť vzájomnú polohu. Náboje nie sú v dielektriku viazané na úplne nemenné polohy. Ich rozloženie sa pôsobením vonkajšieho elektrostatického poľa môže do istej miery meniť. Treba si uvedomiť, že náboj obsiahnutý v látke je veľmi veľký. Už i miligram látky obsahuje približne 50 C kladného a 50 C záporného náboja. I veľmi malé posunutie náboja sa vzhľadom na jeho množstvo môže prejaviť poruchou vzájomnej kompenzácie polí vytvorených nábojmi opačného znamienka a výsledné elektrostatické pole od týchto nábojov už nebude nulové. Tento proces sa nazýva polarizácia dielektrika. Vzhľadom na rôznu štruktúru látok sa polarizácia môže uskutočniť niekoľkými spôsobmi:

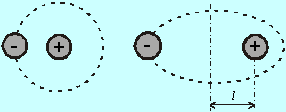
Elektrónová polarizácia (tiež atómová polarizácia). Vzniká vzájomným posuvom kladne nabitého jadra a záporne nabitého elektrónového obalu atómu. Elektróny obiehajú okolo jadra s vysokou frekvenciou, (rýchlosťou porovnateľnou s rýchlosťou svetla). Elektrónový obal sa dá takto považovať za rovnomerne nabitú guľovú vrstvu. Elektrostatické pole v jej okolí je také isté ako pole v okolí bodového rovnako veľkého náboja, ktorý by bol v jej strede. Výsledné pole od jadra a elektrónového obalu je teda nulové. Pôsobením vonkajšieho elektrostatického poľa sa súmernosť molekuly poruší. Jadro je ťahané v smere poľa, elektróny v opačnom smere. Takto nastane deformácia atómu. Stred elektrónového obalu nesplýva so stredom jadra (Obr.8.3.3.1). Atóm sa zmení na elektrický dipól s elektrickým momentom, ktorý je úmerný vzájomnému posunu kladných a záporných nábojov. Toto posunutie je veľmi malé i vzhľadom na vzdialenosti elektrónového obalu od stredu atómu. Elektrické pole jadra v mieste elektrónu má intenzitu ~ 10¹² V m^-1, vonkajšie elektrické pole je minimálne o šesť rádov menšie, preto aj zmena parametrov dráhy je veľmi malá. Príkladom elektrónovej polarizácie je polarizácia atómu inertného plynu, napr. He. Atómová polarizácia vzniká v každej látke, ale v súčinnosti s inými typmi polarizácie (uvedenými nižšie), je to najslabšia časť celkovej polarizácie.

Obr. 8.3.3.1

Atómová polarizácia

Iónová polarizácia. Vzniká v látkach, ktorých molekuly sú zložené z dvoch alebo viacej iónov. Takéto molekuly majú nenulový elektrický moment aj bez pôsobenia vonkajšieho elektrického poľa. Ak usporiadanie molekúl v látke nie je podmienené väzobnými silami sú orientácie momentov elektrických dipólov náhodne orientované a vektorový súčet momentov veľkého počtu molekúl nulový. Aj v tuhých látkach sa v určitom rozmedzí môže meniť vzájomná poloha iónov v molekule. Ak je látka vo vonkajšom elektrostatickom poli, posunú sa kladné ióny vo všetkých molekulách v smere poľa a záporné ióny proti tomuto smeru, takže výsledný elektrický moment aj veľkého počtu molekúl už nie je nulový a jeho smer je rovnobežný so smerom elektrického poľa. Príkladom sú iónové kryštály, napr. NaCl.

Orientačná polarizácia. Vzniká v kvapalinách a v plynoch, kde sa orientácia polárnych molekúl vplyvom zrážok neustále mení. Mení sa teda aj smer elektrických momentov jednotlivých molekúl. Časová stredná hodnota výsledného elektrického momentu molekúl sa rovná nule. Ak vložíme takúto látku do vonkajšieho elektrostatického poľa, pribudne k neusporiadaným točivým momentom pôsobiacim na molekuly vplyvom termického pohybu ešte aj točivý moment, ktorým pôsobí vonkajšie elektrostatické pole na elektrické dipóly molekúl. Tento sa (pozri časť 8.3.1) snaží natočiť každý dipól tak, aby jeho moment mal smer intenzity poľa. Usmerňovací účinok poľa je však stále rušený termickými pohybmi molekúl, a preto je možný len istý stupeň orientácie, ktorý závisí od teploty a od veľkosti elektrostatického poľa. Príkladom orientačnej polarizácie je polarizácia vody, molekula vody má nenulový elektrický dipól.

Ak sa stočia dipólové momenty všetkých molekúl do smeru elektrického poľa, nedá sa orientačná polarizácia už zvýšiť. Naproti tomu atómová a iónová polarizácia môže rásť priamoúmerne s intenzitou poľa, ale len v medziach daných pevnosťou dielektrika.

8.3.3 Vektor polarizácie

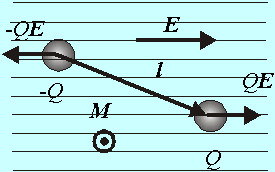
Obr. 8.3.4.1

Polarizácia dielektrika

Pri elektrónovej polarizácii nastáva posunutie všetkých kladných nábojov v smere poľa za súčasného posunutia záporných nábojov proti smeru poľa. Podobné je to aj pri polarizácii iónovej a orientačnej. Zmeny spôsobené v dielektriku vplyvom polarizácie sa dajú pri všetkých typoch polarizácie popísať formálne rovnakým spôsobom. Kladné náboje rozložené v celom priestore dielektrika sa posunú o dĺžku l vzhľadom na náboje záporné (Obr.8.3.4.1). Pole, v ktorom sa malý objem dielektrika ohraničený vzdialenosťou l a plôškou dS_^ nachádza, môžeme považovať za homogénne. Potom aj rozloženie kladného a záporného náboja na plôškach dS_^ má konštantnú plošnú hustotu s_p⁺ resp. s_p^- a pole vzniknuté v takejto elementárnej bunke vplyvom polarizácie je homogénne, také isté ako pole medzi dvoma nekonečne veľkými rovinami nabitými nábojmi opačného znamienka s plošnými hustotami s_p⁺ resp. s_p^- . Intenzita takéhoto poľa je podľa (8.2.3.1)

(8.3.4.1)

kde l₀ je jednotkový vektor polohového vektora l kladného náboja vzhľadom na náboj záporný v takejto bunke. Elektrický moment jedného dipólu v tejto bunke je

a elektrický moment celej bunky je

(8.3.4.2)

kde dt = dS_^l je objem elementárnej bunky. Objemová hustota elektrického momentu v polarizovanom dielektriku sa nazýva elektrická polarizácia (vektor elektrickej polarizácie)

. (8.3.4.3)

Je to elektrický moment pripadajúci na jednotku objemu dielektrika a veľkosť kladného náboja dipólu sa rovná hustote s_p⁺ kladného náboja „vylúčeného“ polarizáciou na hladine bunky. Táto hustota sa nazýva hustota polarizačného náboja. Predpokladajme, že dielektrikum je lineárne, to znamená, že relatívny posun l nábojov v smere poľa je úmerný intenzite poľa. Je to vtedy, ak sily elektrického poľa sú malé oproti väzbovým silám molekúl.

(8.3.4.4)

Potom

.

Po dosadení do (8.3.4.1)

. (8.3.4.5)

Konštanta

(8.3.4.6)

popisujúca vlastnosti dielektrika sa nazýva elektrická susceptibilita. Potom intenzita E_p elektrostatického poľa vytvoreného vplyvom polarizácie je

(8.3.4.7)

a vektor elektrickej polarizácie

. (8.3.4.8)

Hustota polarizačného náboja s_p⁺ vyplýva zo vzťahov (8.3.4.4,2).

. (8.3.4.9)

E vo vzťahoch (8.3.4.7,8,9) je intenzita skutočného poľa, ktoré existuje v dielektriku, to znamená poľa voľných nábojov a poľa vzniknutého vplyvom polarizácie dielektrika. Polarizácia závisí totiž od skutočného poľa a nielen od poľa, ktoré by v danom mieste bolo, keby sa dielektrikum nepolarizovalo. Ak označíme intenzitu poľa, ktoré má pôvod len vo voľných nábojoch okolitých nabitých telies, intenzita skutočného poľa bude

(8.3.4.10)

z toho

(8.3.4.11)

kde konštanta

(8.3.4.12)

sa nazýva relatívna permitivita prostredia.

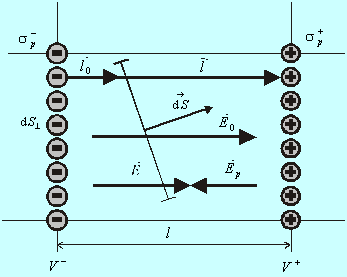
Polarizáciou elementárnej bunky dielektrika vzniknú na jej protiľahlých hladinách vrstvy opačných nábojov s plošnou hustotou s_p, úmernou intenzite poľa. Tieto dve vrstvy nábojov vytvárajú dodatočné pole s intenzitou E_p opačne orientovanou ako intenzita E₀ pôvodného vonkajšieho poľa. Vonkajšie pole sa vplyvom polarizácie bude v bunke zoslabovať. Rovnako sa chová dielektrikum aj v susednej elementárnej bunke, pričom ako bolo ukázané v odseku (8.1.9.1) pre dve opačne nabité plochy, pole mimo takejto bunky je nulové a teda bunky si polia nebudú navzájom ovplyvňovať. Z uvedeného vyplýva, že odvodené výsledky sa dajú zovšeobecniť na ľubovoľný objem.

8.3.4 Vektor elektrickej indukcie

V Maxwellovej teórii elektromagnetického poľa je dôležitý ďalší vektor D, ktorý sa nazýva vektor elektrickej indukcie a definovaný je vzťahom

. (8.3.5.1)

Po dosadení zo vzťahov (8.3.4.8,12) dostávame

(8.3.5.2)

Vektory D aj E sú v  izotropnom prostredí súhlasne rovnobežné. Vyplýva to z toho, že vektor polarizácie P má v izotropnom prostredí rovnaký smer ako E. Vektor E aj skalár e sú závislé od prostredia, o vektore D to však neplatí. Zo vzťahov (8.3.4.10,8.3.5.1) totiž vyplýva

.

Elektrická indukcia je vo všetkých prostrediach rovná súčinu permitivity vákua a intenzity poľa vzbudeného voľnými nábojmi. Na povrchu nabitého vodiča je elektrická indukcia kolmá na povrch a jej veľkosť je podľa Coulombovej vety (8.2.3.1) rovná plošnej hustote voľných nábojov na vodiči

. (8.3.5.3)

Ak je teda pevne daná hustota voľných nábojov, vektor elektrickej indukcie je veličina nezávislá od dielektrika. Jeho jednotka vyplýva zo vzťahu (8.3.5.3)

Podľa vzťahu (8.3.5.1)

,

kde E_o je intenzita poľa voľného náboja. Ak je tento náboj bodový, potom

Intenzita poľa tohoto náboja v dielektriku je

.
Tento vzťah sa líši od vzťahu popisujúceho intenzitu elektrostatického poľa v okolí bodového náboja vo vákuu tým, že miesto permitivity vákua (elektrickej konštanty) tu vystupuje permitivita dielektrika. Z tohoto vyplýva, že vzťahy odvodené pre elektrostatické pole vo vákuu sú platné aj pre pole v dielektriku, ak sa v nich permitivita vákua e_o nahradí permitivitou dielektrika e.

8.3.5 Materiálové charakteristiky dielektrika

Dielektrické materiály v svojej rôznorodosti majú široké uplatnenie nielen v oblasti elektriny, ale aj mechaniky. Sú to materiály, ktorých vlastnosti sa základom zložitých elektro-opticko-mechanických zariadení. Je to dané tým, po popri širokej škále mechanických vlastností sa vyznačujú i rôznorodosťou elektrických vlastnosti, vyjadrených premitivitou. Príkladom aplikácie vlastností dielektrík sú kopírovacie prístroje na princípe tzv. xeroxu

Nasledujúca tabuľka udáva hodnoty relatívnej permitivity podľa druhu látky a typu polarizácie

Typ dielektrickej látky	Typ polarizácie	relatívna permitivita er
Plyn	Elektrónová	1,0002-1,006
Nepolárna kvapalina	elektrónová	1,8-2,3
Polárne kvapaliny, polárne polyméry	elektrónová a orientačná	3-81
Sklá Iónové kryštály Dipólové kryštály	elektrónová iónová orientačná	3-20 4-300 10-300
Nelineárne dielektriká	spontánna polarizácia	>100000

Permitivita výrazne závisí i od štruktúry látky a typu väzby v tuhej látke. Vlastnosti reálnych dielektrík sú preto veľmi rôznorodé.

Príklad 8.3.1 Na rovnako dlhých nitiach sú zavesené v jednom bode dve rovnaké, malé kovové guľôčky. Sú nabité rovnakým nábojom, preto sa odpudzujú . Po vložení guličiek do kvapalného dielektrika sa rozstup medzi guľôčkami nezmení (Obr. 8.3.1.1). Aká je relatívna permitivita dielektrika, ak hustota guličky je r = 1,5 g cm^-3 (napr. priemerná hustota dutej hliníkovej guličky) a hustota kvapaliny r´ = 0,8 g cm^-3 (transformátorový olej)?

Riešenie

Kontrolné otázky